题目内容
已知一个等腰三角形的边长皆为整数,其周长为8,则它的面积为
- A.6
- B.

- C.
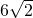
- D.4
B
分析:只需设出腰长,根据三角形的三边关系得到腰长的取值范围,再根据边长皆为整数,求得腰长的值;
然后根据等腰三角形的性质和勾股定理计算其底边上的高,从而求得三角形的面积.
解答:设腰长为x,则底边是8-2x.
根据三角形的三边关系,得0<8-2x<2x,解得2<x<4.
因为边长皆为整数,所以x=3.
即三边为3,3,2.
根据等腰三角形的三线合一和勾股定理,得其底边上的高是2 .
.
则面积为 ×2×
×2× =
= .
.
故选B.
点评:本题考查等腰三角形“三线合一”的性质、勾股定理和三角形的三边关系.
分析:只需设出腰长,根据三角形的三边关系得到腰长的取值范围,再根据边长皆为整数,求得腰长的值;
然后根据等腰三角形的性质和勾股定理计算其底边上的高,从而求得三角形的面积.
解答:设腰长为x,则底边是8-2x.
根据三角形的三边关系,得0<8-2x<2x,解得2<x<4.
因为边长皆为整数,所以x=3.
即三边为3,3,2.
根据等腰三角形的三线合一和勾股定理,得其底边上的高是2
 .
.则面积为
 ×2×
×2× =
= .
.故选B.
点评:本题考查等腰三角形“三线合一”的性质、勾股定理和三角形的三边关系.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知一个等腰三角形的底边长为5,这个等腰三角形的腰长为x,则x的取值范围是( )
A、0<x<
| ||
B、x≥
| ||
C、x>
| ||
| D、0<x<10 |