Question

【题目】如图，在中，点是边上一个动点，过点作直线，设交的平分线于点，交的外角平分线于点．

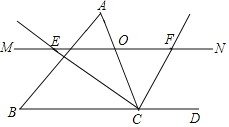
（1）探究与的数量关系并加以证明；
（2）当点运动到上的什么位置时，四边形是矩形，请说明理由；
（3）在（2）的基础上，满足什么条件时，四边形是正方形？为什么？

Answer 1

【答案】（1）OE=OF，理由见解析；（2）当点O运动到AC的中点时，四边形AECF是矩形．理由见解析；（3）当点O运动到AC的中点时，且△ABC满足∠ACB为直角的直角三角形时，四边形AECF是正方形．理由见解析；

【解析】

（1）由平行线的性质和角平分线定义得出∠OEC=∠OCE，∠OFC=∠OCF，根据“等角对等边”得出OE=OC，OF=OC，即可得出结论；
（2）由（1）得出的OE=OC=OF，点O运动到AC的中点时，则由OE=OC=OF=OA，证出四边形AECF是平行四边形，再证出∠ECF=90°即可；
（3）由已知和（2）得到的结论，点O运动到AC的中点时，且△ABC满足∠ACB为直角的直角三角形时，则推出四边形AECF是矩形且对角线垂直，得出四边形AECF是正方形．

（1）OE=OF，理由如下：
∵MN∥BC，
∴∠OEC=∠BCE，∠OFC=∠DCF，
∵CE平分∠BCA，CF平分∠ACD，
∴∠OCE=∠BCE，∠OCF=∠DCF，
∴∠OCE=∠OEC，∠OCF=∠OFC，
∴OE=OC，OF=OC，
∴OE=OF；
（2）解：当点O运动到AC的中点时，四边形AECF是矩形．
∵当点O运动到AC的中点时，AO=CO，
又EO=FO，
∴四边形AECF为平行四边形，
又CE为∠ACB的平分线，CF为∠ACD的平分线，
∴∠BCE=∠ACE，∠ACF=∠DCF，
∴∠BCE+∠ACE+∠ACF+∠DCF=2（∠ACE+∠ACF）=180°，
即∠ECF=90°，
∴四边形AECF是矩形；
（3）解：当点O运动到AC的中点时，且△ABC满足∠ACB为直角的直角三角形时，四边形AECF是正方形．理由如下：
∵由（2）知，当点O运动到AC的中点时，四边形AECF是矩形，
∵MN∥BC，
当∠ACB=90°，则∠AOF=∠COE=∠COF=∠AOE=90°，
∴AC⊥EF，
∴四边形AECF是正方形．