Question

已知：在△ABC中，∠A＝90°，AB＝AC，D为BC的中点，

（1）如图，E，F分别是AB，AC上的点，且BE＝AF，求证：△DEF为等腰直角三角形．

（2）若E，F分别为AB，CA延长线上的点，仍有BE＝AF，其他条件不变，那么△DEF是否仍为等腰直角三角形？证明你的结论．

Answer 1

证明：（1）连结，∵，∠BAC＝90° ，为BC的中点，∴AD⊥BC ，BD＝AD，∴∠B＝∠DAC＝45°             

又BE＝AF，∴△BDE≌△ADF    ∴ED＝FD ，∠BDE＝∠ADF    

∴∠EDF＝∠EDA＋∠ADF＝∠EDA＋∠BDE＝∠BDA＝90°

∴△DEF为等腰直角三角形   

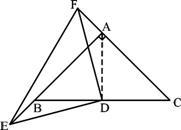（2）若E，F分别是AB，CA延长线上的点，如图所示．

连结AD ，

∵AB＝AC ，∠BAC＝90° ，D为BC的中点

∴AD＝BD ，AD⊥BC ，∴∠DAC＝∠ABD＝45°

∴∠DAF＝∠DBE＝135°，

又AF＝BE，∴△DAF≌△DBE   

∴FD＝ED ，∠FDA＝∠EDB

∴∠EDF＝∠EDB＋∠FDB＝∠FDA＋∠FDB＝∠ADB＝90°…

∴△DEF仍为等腰直角三角形   …9分