题目内容
 如图,在?ABCD中,E是AD的中点,且CE=CD,F是CE与BD的交点,S△DEF=S,则S△BCF=________.
如图,在?ABCD中,E是AD的中点,且CE=CD,F是CE与BD的交点,S△DEF=S,则S△BCF=________.
4S
分析:由四边形ABCD是平行四边形,E是AD的中点,可得△DEF∽△BCF,DE:BC=1:2,然后根据相似三角形面积的比等于相似比的平方,即可求得答案.
解答:∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,
∵E是AD的中点,
∴DE= AD,
AD,
∴DE:BC=1:2,
∵AD∥BC,
∴△DEF∽△BCF,
∴ ,
,
∵S△DEF=S,
∴S△BCF=4S.
故答案为:4S.
点评:此题考查了相似三角形的判定与性质与平行四边形的性质.此题难度不大,解题的关键是掌握相似三角形面积的比等于相似比的平方的定理的应用,注意数形结合思想的应用.
分析:由四边形ABCD是平行四边形,E是AD的中点,可得△DEF∽△BCF,DE:BC=1:2,然后根据相似三角形面积的比等于相似比的平方,即可求得答案.
解答:∵四边形ABCD是平行四边形,
∴BC=AD,AD∥BC,
∵E是AD的中点,
∴DE=
 AD,
AD,∴DE:BC=1:2,
∵AD∥BC,
∴△DEF∽△BCF,
∴
 ,
,∵S△DEF=S,
∴S△BCF=4S.
故答案为:4S.
点评:此题考查了相似三角形的判定与性质与平行四边形的性质.此题难度不大,解题的关键是掌握相似三角形面积的比等于相似比的平方的定理的应用,注意数形结合思想的应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=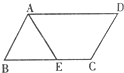 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.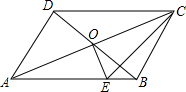 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是