题目内容
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
(1)求证:MA=MB;
(2)探究:在旋转三角尺的过程中,四边形AOBM的面积是否发生变化?若发生变化,请说明理由;若不发生变化,请求出四边形AOBM的面积.

1)证明:如图,过点M作ME⊥OP于点E,作MF⊥OQ于点F,
∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=![]() OQ=2,MF=
OQ=2,MF=![]() OP=2,
OP=2,
∴ME=MF,
∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
 ,
,
∴△AME≌△BMF(ASA),
∴MA=MB;
(2)解:四边形AOBM的面积不发生变化;
理由:由(1)得出:AE=FB,OF=FQ=OE,
∴BQ=FQ﹣BF=EO﹣AE=AO,
∴PA+BQ=PO=5,
∵四边形AOBM的面积为:S△POQ﹣S△MPA﹣S△MQB=![]() ×PO×QO﹣
×PO×QO﹣![]() (PA+BQ)×ME=
(PA+BQ)×ME=![]() ×5×5﹣
×5×5﹣![]() ×5×
×5×![]() =
=![]() .
.


练习册系列答案
相关题目
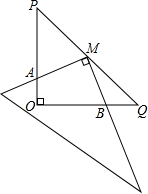 如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=5,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.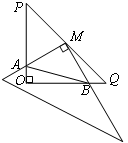

 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.