题目内容
下面的图①、图②分别是一所学校调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图:

根据上图信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若这所学校共有2700名学生,你估计该校有多少名学生知道母亲的生日?
解:(每小题,共6分)
(1)30 =90,条形统计图如图所示;
=90,条形统计图如图所示;

(2)2700× =1500人.
=1500人.
估计该校约有1500名学生知道母亲的生日.
分析:(1)根据记不清的人数与圆心角的度数即可求出总人数,进而可求出知道与不知道的人数,再画图即可解答.
(2)利用样本估计总体的知识解答即可.
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
(1)30
 =90,条形统计图如图所示;
=90,条形统计图如图所示;
(2)2700×
 =1500人.
=1500人.估计该校约有1500名学生知道母亲的生日.
分析:(1)根据记不清的人数与圆心角的度数即可求出总人数,进而可求出知道与不知道的人数,再画图即可解答.
(2)利用样本估计总体的知识解答即可.
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
小刘对本班同学业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图(1)和图(2)
 | |||
 | |||
(1)
(2)
请你根据图中提供的信息,解答下列问题:
(1)在图(1)中,将“书画”部分的图形补充完整;
(2)在图(2)中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图(1)和图(2),你能得出哪些结论,(只要写一条结论)


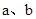 的大小比较,有下面的方法:
的大小比较,有下面的方法: 时,一定有
时,一定有 ;
; 时,一定有
时,一定有 ;
; 时,一定有
时,一定有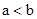 .
.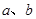 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较: ,
,
 )与(
)与( )的符号相同
)的符号相同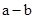 >0,得
>0,得
