题目内容
【题目】在平面直角坐标系中,已知A(3,0),以OA为一边在第一象限内画正方形OABC,D(m,0)为x轴上的一个动点,以BD为一边画正方形BDEF(点F在直线AB右侧).
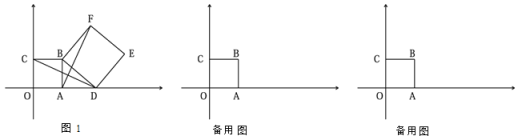
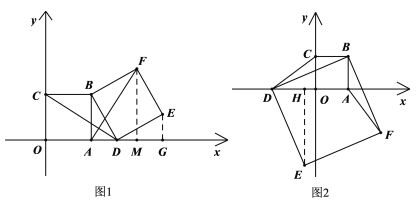
(1)当m>3时(如图1),试判断线段AF与CD的数量关系,并说明理由.
(2)当AF=5时,求点E的坐标;
(3)当D点从A点向右移动4个单位,求这一过程中F点移动的路程是多少?
【答案】(1)![]() ,理由见解析;(2)点E的坐标为
,理由见解析;(2)点E的坐标为![]() 或
或![]() ;(3)这一过程中F点移动的路程是向上移动4个单位.
;(3)这一过程中F点移动的路程是向上移动4个单位.
【解析】
(1)先根据正方形的性质得出![]() ,再根据角的和差求出
,再根据角的和差求出![]() ,然后根据三角形全等的判定定理与性质即可得;
,然后根据三角形全等的判定定理与性质即可得;
(2)分点D在点A的右侧和点D在点A的左侧,分别画出图形.①如图1,先利用(1)的结论可得![]() ,再利用勾股定理求出
,再利用勾股定理求出![]() ,从而可得
,从而可得![]() ,然后过点E作
,然后过点E作![]() 轴于点G,根据三角形全等的判定定理与性质可得
轴于点G,根据三角形全等的判定定理与性质可得![]() ,从而可得
,从而可得![]() ,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出
,由此即可得;②如图2,同①的方法,利用三角形全等的判定定理与性质得出![]() ,从而可得
,从而可得![]() ,由此即可得;
,由此即可得;
(3)参照(2)①的方法,求出点F的坐标,从中可发现点F的坐标与m的关系,由此即可得出答案.
(1)![]() ,理由如下:
,理由如下:
![]() 四边形OABC和四边形BDEF都是正方形
四边形OABC和四边形BDEF都是正方形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,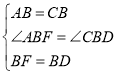
![]()
![]() ;
;
(2)由题意,分以下两种情况:
①如图1,点D在点A的右侧
![]() 四边形OABC和四边形BDEF都是正方形,
四边形OABC和四边形BDEF都是正方形,![]()
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
由(1)可知,![]()
在![]() 中,
中,![]()
![]()
过点E作![]() 轴于点G
轴于点G
在![]() 和
和![]() 中,
中,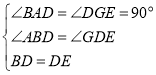
![]()
![]()
![]()
此时点E的坐标为![]()
②如图2,点D在点A的左侧
由(1)可知,![]()
在![]() 中,
中,![]()
![]()
过点E作![]() 轴于点H
轴于点H
同理可证:![]()
![]()
![]()
此时点E的坐标为![]()
综上,点E的坐标为![]() 或
或![]() ;
;
(3)由题意,只需求出点D在点A的右侧,即![]() 时,点F的坐标即可解决问题
时,点F的坐标即可解决问题
如图1,过点F作![]() 轴于点M
轴于点M
由(1)已证:![]()
![]() ,
,![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,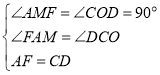
![]()
![]()
![]()
此时点F的坐标为![]()
由此可知,当D点从A点向右移动4个单位时,点F向上移动4个单位
即这一过程中F点移动的路程是向上移动4个单位.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案



