题目内容
【题目】如图，抛物线y= 
x2﹣2x﹣6 
与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点，点E在抛物线上，且横坐标为4 ，AE与y轴交F．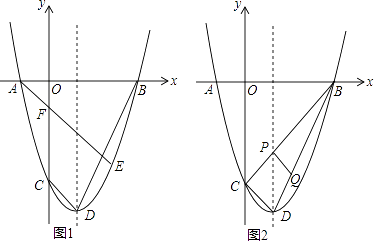
（1）求抛物线的顶点D和F的坐标；
（2）点M，N是抛物线对称轴上两点，且M（2 ，a），N（2 ，a+ ），是否存在a使F，C，M，N四点所围成的四边形周长最小，若存在，求出这个周长最小值，并求出a的值；
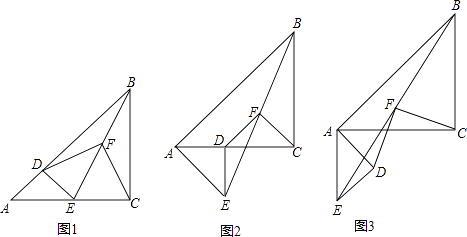
（3）连接BC交对称轴于点P，点Q是线段BD上的一个动点，自点D以2 
个单位每秒的速度向终点B运动，连接PQ，将△DPQ沿PQ翻折，点D的对应点为D′，设Q点的运动时间为t（0≤t≤ 
）秒，求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的 
时对应的t值．
【答案】
（1）
解：∵y= 
x2﹣2x﹣6 
= （x﹣2 ）2﹣8 ，
∴顶点D坐标（2 ，﹣8 ），
由题意E（4 ，﹣8 ），A（﹣2 ，0），B（6 ，0），
设直线AE解析式为y=kx+b，则有 
，解得 
，
∴直线AE解析式为y=﹣x﹣2 ，
∴点F坐标（0，﹣2 ）
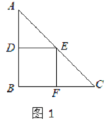
（2）
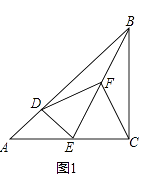
解：如图1中，作点F关于对称轴的对称点F′，连接FF′交对称轴于G，在CF上取一点C′，使得CC′= ，连接C′F′与对称轴交于点N，此时四边形CMNF周长最小．
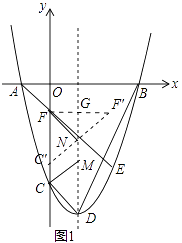
∵四边形CMNF的周长=CF+NM+CM+FN=5 +CM+NF，CM+NF=C′N+NF=C′N+NF′=C′F′（两点之间线段最短），
∴此时四边形CMNF的周长最小．
∵C′F=3
∴GN= 
C′F= 
，
∴﹣（a+ ）=2 + 
，
∴a=﹣ 
，
∵C′F′= 
=5 ，
∴四边形CMNF的周长最小值=5 
+5 =10
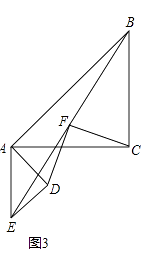
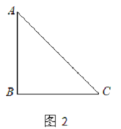
（3）
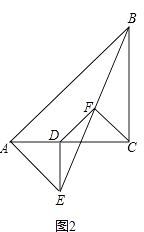
解：如图2中，作PF⊥BD于F，QH⊥对称轴于H．
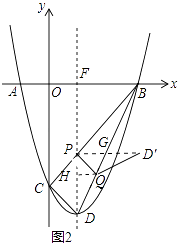
由题意可知BD= 
=4 
，DQ=2 t，
∵S△PQG= S△DPQ= S△PD′Q，
∴PG= PD′= PD=2 = BF，
情形①PG∥FB时，∵PF=PD，
∴BG=GD，
∴PG= BF=2 ，
在Rt△QHD中，sin∠HDQ= ，DQ=2 t，
∴HQ=2 t，HD=4 t，
∵∠QPD′=∠QPD=45°，
∴PH=HQ=2 t，
∴PH+HD=PD，
∴6 t=4 ，
∴t= 
．
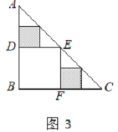
情形②如图3中，PG′=PG=2 ，作PM⊥BD于M，QK⊥PD于K，QJ⊥PD′于J．
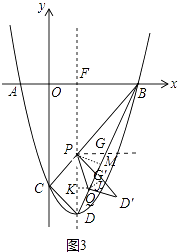
由sin∠PDG=sin∠GPM= 
= 
，
∴MG′=MG= 
，
∴G′D=BD﹣GG′= 
，
∵ 
= 
= 
，
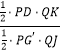∵∠QPD=∠QPG′，QK⊥PD，QJ⊥PG′，
∴QK=QJ，
∴ = 
=2，
∴QD= × = 
，
∴t= 
= 
，
综上所述t= 或 秒时，△D′PQ与△PQB重叠部分的面积为△DPQ面积的
【解析】（1）利用配方法或公式法求顶点坐标，求出最小AE即可求出点F坐标．（2）如图1中，作点F关于对称轴的对称点F′，连接FF′交对称轴于G，在CF上取一点C′，使得CC′= ，连接C′F′与对称轴交于点N，此时四边形CMNF周长最小．（3）分两种情形①PG∥FB时；②如图3中，PG′=PG=2 ，作PM⊥BD于M，QK⊥PD于K，QJ⊥PD′于J．分别求解即可．
【考点精析】通过灵活运用二次函数的图象，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点即可以解答此题．
