题目内容
已知两个全等的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,AB=DE=4.(1)若纸片△DEF不动,把△ABC绕点F逆时针旋转30°时,连结CD,AE,如图2.
①求证:四边形ACDE为梯形;
②求四边形ACDE的面积.
(2)将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,直接写出△ABC恰有一边与DE平行的时间.(写出所有可能的结果)

【答案】分析:(1)①求出∠FOD=∠ACB=90°,推出AC∥DE,根据梯形判定推出即可;
②求出FO,求出BO,求出梯形高CO,根据梯形面积公式求出即可;
(2)当t=3时,AC∥DE,当t=12时,BC∥DE,当t=15时,AB∥DE、当t=21时,AC∥DE、当t=30时,BC∥DE,当t=33时,AB∥DE.
解答:(1)①证明:如图2,∵∠BFD=30°、∠EDF=60°,
∴∠FOD=90°=∠ACB,
∴AC∥BD,且AC≠BD,
∴四边形ACDE为梯形;
②解:BC交DE于O,在Rt△FDO中,FD=2,∠OFD=30°
∴FO= ,而CF=2
,而CF=2 -2
-2
∴CO=3 -2,
-2,
∴S四边形ACDE= ×(2+4)×(3
×(2+4)×(3 -2)=9
-2)=9 -6;
-6;
(2)解:△ABC恰有一边与DE平行的时间是:3、12、15、21、30、33.
点评:本题考查了勾股定理,梯形的性质和判定,三角形的内角和定理,旋转的性质的应用,主要考查学生综合运用性质进行推理和计算的能力.
②求出FO,求出BO,求出梯形高CO,根据梯形面积公式求出即可;
(2)当t=3时,AC∥DE,当t=12时,BC∥DE,当t=15时,AB∥DE、当t=21时,AC∥DE、当t=30时,BC∥DE,当t=33时,AB∥DE.
解答:(1)①证明:如图2,∵∠BFD=30°、∠EDF=60°,

∴∠FOD=90°=∠ACB,
∴AC∥BD,且AC≠BD,
∴四边形ACDE为梯形;
②解:BC交DE于O,在Rt△FDO中,FD=2,∠OFD=30°
∴FO=
 ,而CF=2
,而CF=2 -2
-2∴CO=3
 -2,
-2,∴S四边形ACDE=
 ×(2+4)×(3
×(2+4)×(3 -2)=9
-2)=9 -6;
-6;(2)解:△ABC恰有一边与DE平行的时间是:3、12、15、21、30、33.
点评:本题考查了勾股定理,梯形的性质和判定,三角形的内角和定理,旋转的性质的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
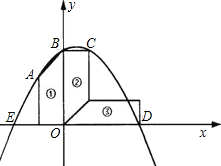 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.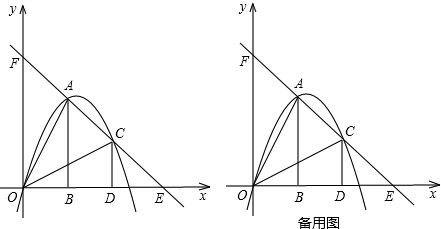
 x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
x2-bx-c经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6.
