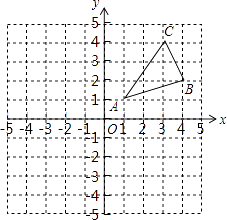Question

【题目】如图，直线y=kx﹣1与x轴、y轴分别交于B、C两点，且3BO﹣ CO=1

（1）求点B的坐标及k的值；
（2）若点A（x，y）是第一象限内的直线y=kx﹣1上的一个动点，在点A的运动过程中，试写出△AOB的面积S与x之间的函数解析式；
（3）探索：当点A运动到什么位置时，△AOB的面积是 ？

Answer 1

【答案】
（1）解：当x=0时，y=kx﹣1=﹣1，则C（0，﹣1），

当y=0时，kx﹣1=0，解得x= ，则B（ ，0），

∵3BO﹣ CO=1

∴ ﹣ =1，

∴k=2，

∴B（ ，0）

（2）解：y= x﹣1，

S= （ x﹣1）

= x﹣ （x＞ ）

（3）解：设A（x， x﹣1），

∵S= | x﹣1|，

∴ | x﹣1|= ，解得x=4或x=0，

∴A点坐标为（4，1）或（0，1），

即A点运动到（4，1）或（0，1）位置时，△AOB的面积是

【解析】（1）利用坐标轴上点的坐标特征和一次函数图象上点的坐标特征先得到C（0，﹣1），B（ ，0），则利用3BO﹣ CO=1得到 ﹣ =1，解方程得到k的值，从而得到B点坐标；（2）A点坐标表示为（x， x﹣1），然后利用三角形面积公式求解；（3）设A（x， x﹣1），利用三角形面积公式得到 | x﹣1|= ，然后解绝对值方程得到x的值，从而得到A点坐标．
【考点精析】本题主要考查了一次函数的性质的相关知识点，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小才能正确解答此题．