题目内容
三角形的三条外角平分线所在直线相交构成的三角形一定是什么形状的三角形?请说明理由.分析:根据三角形的外角的性质可表示出∠B1AC+∠B1CA,再根据三角形内角和定理可表示出∠B1,同理可表示出∠A1,∠C1,从而不难判断△A1B1C1的形状.
解答: 解:锐角三角形.
解:锐角三角形.
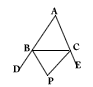
如图A1,B1,C1分别△ABC三个外角平分线的交点.
∴∠B1AC+∠B1CA=
(∠BAC+∠BCA+∠ABC+∠ABC)=
(180°+∠ABC),
∴∠B1=180°-
(180°+∠ABC)=90°-
∠ABC<90°,
同理:∠C1=90°-
∠ACB<90°,
∠A1=90°-
∠BAC<90°,
∴△A1B1C1一定是锐角三角形.
 解:锐角三角形.
解:锐角三角形.如图A1,B1,C1分别△ABC三个外角平分线的交点.
∴∠B1AC+∠B1CA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠B1=180°-
| 1 |
| 2 |
| 1 |
| 2 |
同理:∠C1=90°-
| 1 |
| 2 |
∠A1=90°-
| 1 |
| 2 |
∴△A1B1C1一定是锐角三角形.
点评:此题主要考查三角形外角的性质及三角形内角和定理的综合运用.

练习册系列答案
相关题目
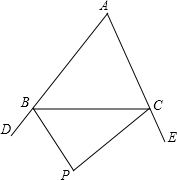 如图,PB和PC是△ABC的两条外角平分线.
如图,PB和PC是△ABC的两条外角平分线. 如图,PB和PC是△ABC的两条外角平分线.
如图,PB和PC是△ABC的两条外角平分线. ∠BAC.
∠BAC.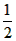 ∠BAC;
∠BAC;