题目内容
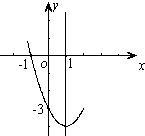 7、已知,抛物线y=ax2+bx+c的部分图象如图,则下列说法①对称轴是直线x=1;②当-1<x<3时,y<0;③a+b+c=-4;④方程ax2+bx+c+5=0无实数根.其中正确的有( )
7、已知,抛物线y=ax2+bx+c的部分图象如图,则下列说法①对称轴是直线x=1;②当-1<x<3时,y<0;③a+b+c=-4;④方程ax2+bx+c+5=0无实数根.其中正确的有( )分析:①可直接观察得对称轴;②由点(-1,0)及对称轴x=1,可得另一交点(3,0),从而判断y<0时,x的范围;③设交点式,把点(0,-3)代入可求抛物线解析式,判断a+b+c的值;④可求出顶点坐标为(1,-4),就能知道y=ax2+bx+c的最小值是-4,ax2+bx+c+5≥1,方程无实数根.
解答:解:①、由图象可知,对称轴是直线x=1,正确;
②、对称轴是直线x=1,抛物线与x轴的一个交点是(-1,0),则另一个交点是(3,0),所以当-1<x<3时,y<0,正确;
③、已知点(-1,0),(3,0),设抛物线的交点式y=a(x+1)(x-3),再把点(0,-3)代入得a=1,所以y=(x+1)(x-3)=x2-2x-3,故a+b+c=1-2-3=-4,正确;
④因为y=x2-2x-3=(x-1)2-4≥-4,所以y+5≥1,即ax2+bx+c+5≥1,方程无实数根,正确.
故选D.
②、对称轴是直线x=1,抛物线与x轴的一个交点是(-1,0),则另一个交点是(3,0),所以当-1<x<3时,y<0,正确;
③、已知点(-1,0),(3,0),设抛物线的交点式y=a(x+1)(x-3),再把点(0,-3)代入得a=1,所以y=(x+1)(x-3)=x2-2x-3,故a+b+c=1-2-3=-4,正确;
④因为y=x2-2x-3=(x-1)2-4≥-4,所以y+5≥1,即ax2+bx+c+5≥1,方程无实数根,正确.
故选D.
点评:综合考评了二次函数的图象和性质中的对称性,以及待定系数法求抛物线方程及顶点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
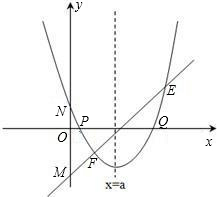 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.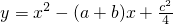 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边.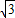 ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.