题目内容
【题目】已知∠A为锐角,
证明:(1)sin A=cos (90°-∠A);
(2)sin2 A+cos2 A=1;
(3)tan A=![]() .
.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析:
如图,把∠A放到Rt△ABC(∠C=90°)中去,利用“锐角三角函数的定义”可得:![]() ,利用这些式子结合“勾股定理”和
,利用这些式子结合“勾股定理”和
“∠A+∠B=90°”就可证得这些等式是成立的.
试题解析:
作Rt△ABC,使∠C=90°,如图,
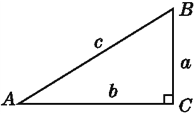
则sin A=![]() ,cos A=
,cos A=![]() ,tan A=
,tan A=![]() .
.
(1)∵cos B=![]() ,sin A=
,sin A=![]() ,
,
∴ sin A=cos B.
又∵∠A+∠B=90°,
∴∠B=90°-∠A,
∴sin A=cos (90°-∠A).
(2)∵sin A=![]() ,cos A=
,cos A=![]() ,且a2+b2=c2,
,且a2+b2=c2,
∴ sin2A+cos2A=![]() +
+![]() =
=![]() =
=![]() =1.
=1.
(3)∵sin A=![]() ,cos A=
,cos A=![]() ,
,
∴ ![]() =
=![]() =
=![]() .
.
又∵tan A=![]() ,
,
∴tan A=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目