题目内容
D是△ABC中AB边上一点，连接CD，∠B=∠ACD，当∠ACB与∠ADC互为余角时，∠BDC=________．
135°
分析：根据三角形内角和外角的关系，确定∠3=∠1+∠B，又因为∠B=∠2，得到∠3=∠1+∠2，然后根据∠ACB+∠ADC=90°，求出∠1+∠2的值，进而可求出∠BDC．
解答：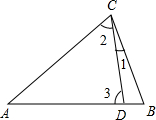
解：因为∠3=∠1+∠B，∠B=∠2，
∴∠3=∠1+∠2，
又∵∠ACB+∠ADC=90°，
则∠1+∠2+∠3=90°，
即（∠1+∠2）+（∠1+∠2）=90°，
故∠1+∠2=45°，
又∵∠B=∠2，
∴∠1+∠B=45°，
于是∠BDC=180°-45°=135°．
点评：此题考查了三角形内角和外角的关系、两角的互余关系等内容，关键是根据∠ACB与∠ADC互余建立起各角之间的关系．
分析：根据三角形内角和外角的关系，确定∠3=∠1+∠B，又因为∠B=∠2，得到∠3=∠1+∠2，然后根据∠ACB+∠ADC=90°，求出∠1+∠2的值，进而可求出∠BDC．
解答：
解：因为∠3=∠1+∠B，∠B=∠2，∴∠3=∠1+∠2，
又∵∠ACB+∠ADC=90°，
则∠1+∠2+∠3=90°，
即（∠1+∠2）+（∠1+∠2）=90°，
故∠1+∠2=45°，
又∵∠B=∠2，
∴∠1+∠B=45°，
于是∠BDC=180°-45°=135°．
点评：此题考查了三角形内角和外角的关系、两角的互余关系等内容，关键是根据∠ACB与∠ADC互余建立起各角之间的关系．
练习册系列答案
相关题目
（2012•朝阳区二模）如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形，M、N分别是CE、CF的中点．
