题目内容
已知:如图,正方形ABCD中,点E是BA延长线上一点,连接DE,点F在DE上且DF=DC,DG⊥CF于G. DH平分∠ADE交CF于点H,连接BH.
(1)若DG=2,求DH的长;
(2)求证:BH+DH=![]() CH.
CH.

1)∵DG⊥CF且DF=CD
 ∴∠FDG=
∴∠FDG=![]() ∠FDC.................1分
∠FDC.................1分
∵DH平分∠ADE
∴∠FDH=![]() ∠ADF.................2分
∠ADF.................2分
∴∠HDG=∠FDG-∠FDH![]() =
=![]() ∠FDC-
∠FDC-![]() ∠ADF
∠ADF
=![]() (∠FDC-∠ADF)=
(∠FDC-∠ADF)=![]() ∠ADC=45°....3分
∠ADC=45°....3分
∴△DGH为等腰直角三角形
∵DG=2,
∴DH=![]() .................5分
.................5分
(2)过点C作CM⊥CH, 交HD延长线于点M
∵∠1+∠DCH=∠2+∠DCH=900
∴∠1=∠2
又△DGH为等腰直角三角形
∴△MCH为等腰直角三角形
∴MC=HC
又∵四边形ABCD为正方形
∴CD=CB
∴△MCD≌△HCB .................8分
∴DM=BH
又∵△MCH为等腰直角三角形
∴DM+DH=![]() CH
CH
∴BH+DH=![]() CH .................10分
CH .................10分

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.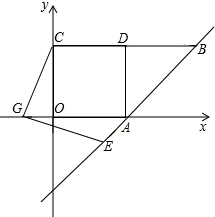
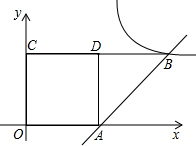
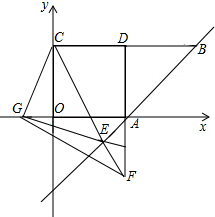



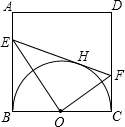 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.