题目内容
如图,抛物线F: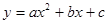 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: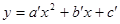 ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.
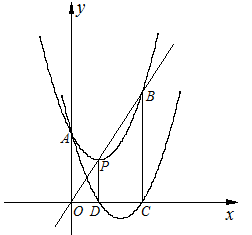
⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了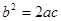
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
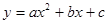 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: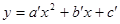 ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.
⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了
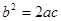
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
解:(1) C(3,0);
(2)①抛物线 ,令
,令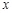 =0,则
=0,则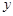 =
=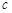 ,
,
∴A点坐标(0,c).
∵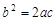 ,∴
,∴ 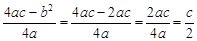 ,
,
∴点P的坐标为(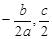 ).
).
∵PD⊥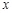 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为(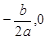 ).
).
根据题意,得a=a′,c= c′,∴抛物线F′的解析式为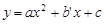 .
.
又∵抛物线F′经过点D(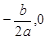 ),∴
),∴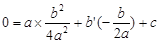 .
.
∴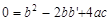 .
.
又∵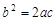 ,∴
,∴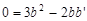 .
.
∴b:b′=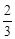 .
.
②由①得,抛物线F′为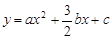 .
.
令y=0,则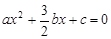 .
.
∴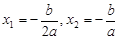 .
.
∵点D的横坐标为 ∴点C的坐标为(
∴点C的坐标为(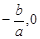 ).
).
设直线OP的解析式为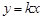 .
.
∵点P的坐标为(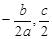 ),
),
∴ ,∴
,∴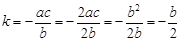 ,∴
,∴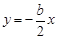 .
.
∵点B是抛物线F与直线OP的交点,∴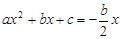 .
.
∴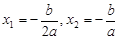 .
.
∵点P的横坐标为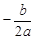 ,∴点B的横坐标为
,∴点B的横坐标为 .
.
把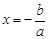 代入
代入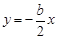 ,得
,得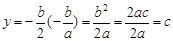 .
.
∴点B的坐标为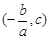 .
.
∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
∴四边形OABC是平行四边形.
又∵∠AOC=90°,∴四边形OABC是矩形.
(2)①抛物线
 ,令
,令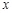 =0,则
=0,则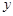 =
=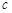 ,
, ∴A点坐标(0,c).
∵
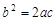 ,∴
,∴ 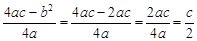 ,
,∴点P的坐标为(
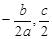 ).
). ∵PD⊥
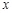 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为(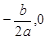 ).
).根据题意,得a=a′,c= c′,∴抛物线F′的解析式为
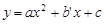 .
.又∵抛物线F′经过点D(
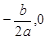 ),∴
),∴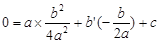 .
.∴
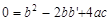 .
.又∵
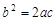 ,∴
,∴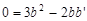 .
.∴b:b′=
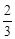 .
.②由①得,抛物线F′为
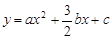 .
.令y=0,则
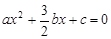 .
.∴
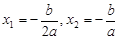 .
.∵点D的横坐标为
 ∴点C的坐标为(
∴点C的坐标为(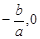 ).
). 设直线OP的解析式为
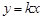 .
.∵点P的坐标为(
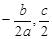 ),
),∴
 ,∴
,∴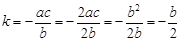 ,∴
,∴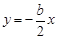 .
.∵点B是抛物线F与直线OP的交点,∴
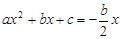 .
.∴
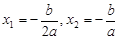 .
.∵点P的横坐标为
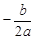 ,∴点B的横坐标为
,∴点B的横坐标为 .
.把
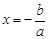 代入
代入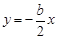 ,得
,得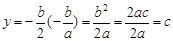 .
.∴点B的坐标为
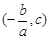 .
.∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
∴四边形OABC是平行四边形.
又∵∠AOC=90°,∴四边形OABC是矩形.
(1)先求出抛物线解析式,再根据平移的特征即可得到点C的坐标;
(2)①根据抛物线顶点坐标的表达式及抛物线与坐标轴的交点坐标的特征即可得到结果;
②根据抛物线与坐标轴的交点坐标及抛物线与直线OP的交点坐标的特征即可得到结果;
(2)①根据抛物线顶点坐标的表达式及抛物线与坐标轴的交点坐标的特征即可得到结果;
②根据抛物线与坐标轴的交点坐标及抛物线与直线OP的交点坐标的特征即可得到结果;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 (
( )的图象如图所示,有下列结论:①
)的图象如图所示,有下列结论:① ;②
;② ;③
;③ ;④
;④ .其中,正确结论的个数是
.其中,正确结论的个数是
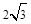 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=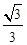 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。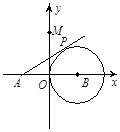
 ,
, 的点共有 个;
的点共有 个;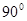 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
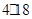 烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度
烟花三月经贸旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度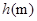 与飞行时间
与飞行时间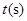 的关系式是
的关系式是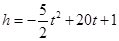 ,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )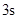
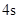
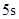
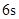
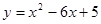 的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线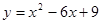 .
.
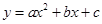 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法: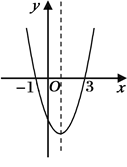
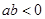 ;②方程
;②方程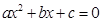 的根为
的根为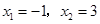 ;
;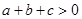 ;④当
;④当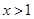 时,y随x值的增大而增大;
时,y随x值的增大而增大; 时,
时,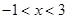 .
.