题目内容
已知:在△ABC中,∠C=90°,AC=4,BC=3,动点P从点A出发,以每秒 个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
个单位的速度沿AB方向向终点B运动;同时,动点Q也从点A出发,以每秒1个单位的速度沿AC方向向终点C运动.设两点运动的时间为t秒(0<t<4).
(1)连接PQ,在点P、Q运动过程中,△APQ与△ABC是否始终相似?请说明理由;
(2)连接PC,设△PCQ的面积为S,求S关于t的函数关系式;
(3)连接PC、BQ,是否存在t的值,使PC⊥BQ?若存在,求出t的值;若不存在,请说明理由;
(4)探索:把△PQB沿直线PQ折叠成△PQB′,设QB′与AB交于点E,当△BEQ是直角三角形时,请直接写出t的值.
解:(1)相似
∵∠ACB=90°
∴AB= =5
=5
∵PA=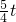 ,AQ=t
,AQ=t
∴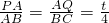
∵∠A=∠A
∴△APQ∽△ABC
(2)∵△APQ∽△ABC
∴∠PQA=∠C=90°
∵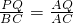
∴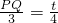
∴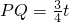
∵CQ=4-t
∴S= =
=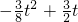
(3)存在
∵PC⊥BQ
∴∠PCQ+∠BQC=90°
∵∠CBQ+∠BQC=90°
∴∠PCQ=∠CBQ
∵∠PQC=∠BCQ=90°
∴△PCQ∽△QBC
∴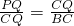
∴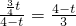
∴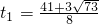 (舍去)
(舍去)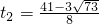
∴存在t的值为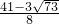 ,使PC⊥BQ.
,使PC⊥BQ.
(4)t1=1,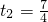 .
.
分析:(1)已知AC、BC的长,根据勾股定理即可求得AB的长,根据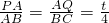 ,进而即可求得△APQ∽△ABC;
,进而即可求得△APQ∽△ABC;
(2)根据△APQ∽△ABC即可求得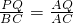 ,即可求得S关于t的方程式;
,即可求得S关于t的方程式;
(3)先求证△PCQ∽△QBC进而可以得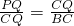 即
即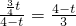 ,求得t的值即可解题.
,求得t的值即可解题.
(4)分别用t表示PE、EQ、BQ的值,根据勾股定理即可求得t的值,即可解题.
点评:本题考查了勾股定理在直角三角形中的运用,考查了相似三角形对应边比值相等的性质,考查了相似三角形的证明,本题中求△PCQ∽△QBC是解题的关键.
∵∠ACB=90°
∴AB=
 =5
=5∵PA=
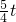 ,AQ=t
,AQ=t∴
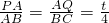
∵∠A=∠A
∴△APQ∽△ABC
(2)∵△APQ∽△ABC
∴∠PQA=∠C=90°
∵
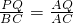
∴
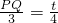
∴
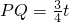
∵CQ=4-t
∴S=
 =
=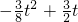
(3)存在
∵PC⊥BQ
∴∠PCQ+∠BQC=90°
∵∠CBQ+∠BQC=90°
∴∠PCQ=∠CBQ
∵∠PQC=∠BCQ=90°
∴△PCQ∽△QBC
∴
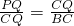
∴
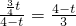
∴
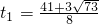 (舍去)
(舍去)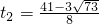
∴存在t的值为
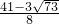 ,使PC⊥BQ.
,使PC⊥BQ.(4)t1=1,
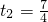 .
.分析:(1)已知AC、BC的长,根据勾股定理即可求得AB的长,根据
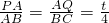 ,进而即可求得△APQ∽△ABC;
,进而即可求得△APQ∽△ABC;(2)根据△APQ∽△ABC即可求得
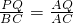 ,即可求得S关于t的方程式;
,即可求得S关于t的方程式;(3)先求证△PCQ∽△QBC进而可以得
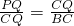 即
即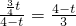 ,求得t的值即可解题.
,求得t的值即可解题.(4)分别用t表示PE、EQ、BQ的值,根据勾股定理即可求得t的值,即可解题.
点评:本题考查了勾股定理在直角三角形中的运用,考查了相似三角形对应边比值相等的性质,考查了相似三角形的证明,本题中求△PCQ∽△QBC是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.