题目内容
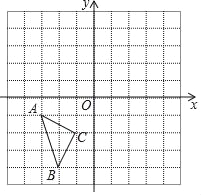
【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= ![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.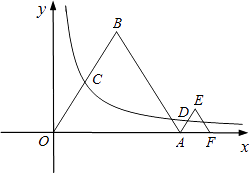
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
【答案】
(1)
解:过点C作CG⊥OA于点G,
∵点C是等边△OAB的边OB的中点,
∴OC=2,∠AOB=60°,
∴OG=1,CG=OGtan60°=1 ![]() =
= ![]() ,
,
∴点C的坐标是(1, ![]() ),
),
由 ![]() =
= ![]() ,得:k=
,得:k= ![]() ,
,
∴该双曲线所表示的函数解析式为y= ![]()

(2)
解:过点D作DH⊥AF于点H,设AH=a,则DH= ![]() a.
a.

∴点D的坐标为(4+a, ![]() a),
a),
∵点D是双曲线y= ![]() 上的点,
上的点,
由xy= ![]() ,得
,得 ![]() a(4+a)=
a(4+a)= ![]() ,
,
即:a2+4a﹣1=0,
解得:a1= ![]() ﹣2,a2=﹣
﹣2,a2=﹣ ![]() ﹣2(舍去),
﹣2(舍去),
∴AD=2AH=2 ![]() ﹣4,
﹣4,
∴等边△AEF的边长是2AD=4 ![]() ﹣8
﹣8
【解析】(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用 待定系数法求反比例函数解析式列式计算即可得解;(2)过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解.

【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: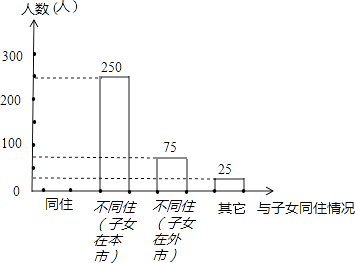
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.