题目内容
【题目】观察理解，并解决问题.
问题情境：如图所示，用一些相同的小正方形，拼在一起，排成如下的一些大正方形：
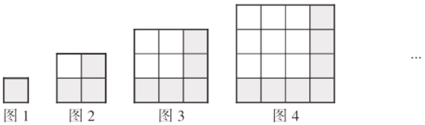
问题解决：（1）完成下表：
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
（2）根据图形规律推测：
______（用含
的代数式表示）
（3）像（1），（2）这样，根据某类事物的部分对象具有的某种性质，推出这类事物的所有对象具有的这种性质的推理，叫做归纳推理.对于科学的发现，归纳推理是十分有用的，通过观察、实验，对有限个对象的性质作归纳整理，提出对某类事物带有规律性的猜测，是科学研究的基本方法.请观察下列等式的规律：第一个等式：
；第二个等式：
；第三个等式：
；…猜想并直接写出第个等式.（用含的代数式表示）
【答案】（1）4，7，n,2n-1；（2）
；（3）
【解析】
（1）根据图形可填写第4列，分析前4列的规律可填写第n列；
（2）根据有理数的加法法则计算即可；
（3）根据所给三个等式归纳出结论即可.
解：（1）
图序号 | 1 | 2 | 3 | 4 | … |
|
一边上小正方形的个数 | 1 | 2 | 3 | 4 | … |
|
阴影小正方形的个数 | 1 | 3 | 5 | 7 | … |
|
（2）
=
=
=；
（3）∵第一个等式：
；
第二个等式：
；
第三个等式：
；
…；
∴第
个等式是：.
字词句段篇系列答案
【题目】某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人(不设弃权票)，选出了票数最多的甲、乙、丙三人.投票结果统计如图一：
其次，对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题：
(1)补全图一和图二；
(2)请计算每名候选人的得票数；
(3)若每名候选人得一票记1分，投票、笔试、面试三项得分按照2:5:3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁?
