题目内容
（2010•南浔区模拟）（1）计算：
+2-1-6tan30°
（2）解方程：x（x-3）-x+3=0．
| 12 |
（2）解方程：x（x-3）-x+3=0．
分析：（1）根据二次根式的化简，特殊角的三角函数以及负指数幂的知识，即可求得答案；
（2）利用因式分解法即可将原方程变为（x-3）（x-1）=0，继而可求得此方程的根．
（2）利用因式分解法即可将原方程变为（x-3）（x-1）=0，继而可求得此方程的根．
解答：解：（1）
+2-1-6tan30°=2
+
-6×
=2
+
-2
=
；
（2）∵x（x-3）-x+3=0，
∴（x-3）（x-1）=0，
∴x-3=0或x-1=0，
解得：x1=3，x2=1．
| 12 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
（2）∵x（x-3）-x+3=0，
∴（x-3）（x-1）=0，
∴x-3=0或x-1=0，
解得：x1=3，x2=1．
点评：此题考查了实数的混合运算，以及因式分解法解一元二次方程的知识．此题比较简单，解题的关键是注意解题需细心，注意掌握二次根式的化简，特殊角的三角函数以及负指数幂的知识，注意提公因式法分解因式的知识．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
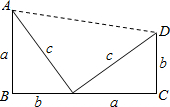（2010•南浔区模拟）利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理，此证明方法就是美国第二十任总统伽菲尔德最先完成的，人们为了纪念他，把这一证法称为“总统”证法．这个定理称为
（2010•南浔区模拟）如图，在直角坐标系中，已知P0的坐标为（1，0），将线段OP0绕O按逆时针方向旋转45°，再将其长度伸长为OP0的3倍，得到线段OP1；又将线段OP1绕O点按逆时针方向旋转45°，长度伸长为OP1的3倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，Opn（n为正整数），则△P2009OP2010的面积
