题目内容
(2012•宽城区一模)如图,在平面直角坐标系中,直线y=-
x+3分别交x轴、y轴于A、B两点.点C在第二象限,⊙C与直线AB和x轴分别相切于E、F两点,连接CE、CF.

(1)如图①,点D为线段AB上一点,⊙C的半径为
.若△CDE∽△BAO,求点D的坐标.
(2)如图②,连接BC,当BC∥x轴时,求点C的坐标.
| 3 |
| 4 |

(1)如图①,点D为线段AB上一点,⊙C的半径为
| 3 |
| 2 |
(2)如图②,连接BC,当BC∥x轴时,求点C的坐标.
分析:(1)根据切线的性质得CF⊥AF,CE⊥AE,再利用相似的性质由△CDE∽△BAO得到∠CDE=∠OAB,则CD∥AF,于是D点的纵坐标为
,然后把D点纵坐标代入直线解析式即可得到D点的横坐标;
(2)先确定A点坐标(4,0),B点坐标(0,3),由于⊙C与直线AB和x轴分别相切于E、F两点,得到CF⊥AF,CE⊥AE,所以四边形BCFO为矩形,则CF=OB=3,得到CE=CF=3,
易证得△BCE≌△AOB,则CB=OA=4,然后可写出C点坐标.
| 3 |
| 2 |
(2)先确定A点坐标(4,0),B点坐标(0,3),由于⊙C与直线AB和x轴分别相切于E、F两点,得到CF⊥AF,CE⊥AE,所以四边形BCFO为矩形,则CF=OB=3,得到CE=CF=3,
易证得△BCE≌△AOB,则CB=OA=4,然后可写出C点坐标.
解答:解:(1)∵⊙C与直线AB和x轴分别相切于E、F两点,
∴CF⊥AF,CE⊥AE,
∵△CDE∽△BAO,
∴∠CDE=∠OAB,
∴CD∥AF,
∵⊙C的半径为
,即CF=
,
∴D点的纵坐标为
,
把y=
代入y=-
x+3得-
x+3=
,解得x=2,
∴D点坐标为(2,
);
(2)把x=0代入y=-
x+3得y=3;把y=0代入-
x+3得-
x+3=0,解得x=4,
∴A点坐标为(4,0),B点坐标为(0,3),
∵⊙C与直线AB和x轴分别相切于E、F两点,
∴CF⊥AF,CE⊥AE,
∴四边形BCFO为矩形,
∴CF=OB=3,
∴CE=CF=3,
在△BCE和△AOB中
,
∴△BCE≌△AOB,
∴CB=OA=4,
∴C点坐标为(-4,3).
∴CF⊥AF,CE⊥AE,
∵△CDE∽△BAO,
∴∠CDE=∠OAB,
∴CD∥AF,
∵⊙C的半径为
| 3 |
| 2 |
| 3 |
| 2 |
∴D点的纵坐标为
| 3 |
| 2 |
把y=
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
∴D点坐标为(2,
| 3 |
| 2 |
(2)把x=0代入y=-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴A点坐标为(4,0),B点坐标为(0,3),
∵⊙C与直线AB和x轴分别相切于E、F两点,
∴CF⊥AF,CE⊥AE,
∴四边形BCFO为矩形,
∴CF=OB=3,
∴CE=CF=3,
在△BCE和△AOB中
|
∴△BCE≌△AOB,
∴CB=OA=4,
∴C点坐标为(-4,3).
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;常利用三角形相似或全等求线段的长;明确求点的坐标就是求有关线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.
(2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.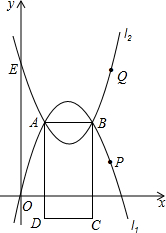 有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.
有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.