题目内容
如图，已知AD∥BC，点E在AC上且AE=3EC，连接DE并延长它，交BC于点F，交AB的延长线于点G．（1）试说明：△ADE∽△CFE；
（2）当EF=2时，
①求
| AD |
| CF |
②当点F恰好是BC的中点时，求GF的长；
（3）当
| CF |
| BF |
| GD |
| GF |
分析：（1）根据AD∥BC，得出∠D=∠EFC，∠DAE=∠C，即可得出△ADE∽△CFE；
（2）①利用相似三角形的性质得出
=
=
，再利用AE=3EC，得出即可；
②首先得出△AGD∽△BGF，进而求出
=2，即可得出GF的长；
（3）由
=3，
=3，得出
•
=9，即可得出答案．
（2）①利用相似三角形的性质得出
| AD |
| CF |
| DE |
| FE |
| AE |
| CE |
②首先得出△AGD∽△BGF，进而求出
| FD |
| GF |
（3）由
| AD |
| CF |
| FC |
| BF |
| AD |
| CF |
| FC |
| BF |
解答：解：（1）∵AD∥BC，
∴∠D=∠EFC，∠DAE=∠C，
∴△ADE∽△CFE．
（2）①∵△ADE∽△CFE，
∴
=
=
．
∵AE=3EC，
∴
=3，
∴
=3，DE=3FE=3×2=6．
②∵点F是BC的中点，
∴BF=CF．
∵
=3，
∴
=3．
∵AD∥BC，
∴△AGD∽△BGF，
∴
=
=3
∴
=2．
由①可知：FD=FE+ED=2+6=8，
∴GF=4．
（3）当
=3时，
=9，理由如下：
∵
=3，
=3，
∴
•
=9，
即
=9，
∴
=
=9．
∴∠D=∠EFC，∠DAE=∠C，
∴△ADE∽△CFE．
（2）①∵△ADE∽△CFE，
∴
| AD |
| CF |
| DE |
| FE |
| AE |
| CE |
∵AE=3EC，
∴
| AE |
| CE |
∴
| AD |
| CF |
②∵点F是BC的中点，
∴BF=CF．
∵
| AD |
| CF |
∴
| AD |
| BF |
∵AD∥BC，
∴△AGD∽△BGF，
∴
| GD |
| GF |
| AD |
| BF |
∴
| FD |
| GF |
由①可知：FD=FE+ED=2+6=8，
∴GF=4．
（3）当
| CF |
| BF |
| GD |
| GF |
∵
| AD |
| CF |
| FC |
| BF |
∴
| AD |
| CF |
| FC |
| BF |
即
| AD |
| BF |
∴
| GD |
| GF |
| AD |
| BF |
点评：此题主要考查了相似三角形的判定与性质，熟练利用相似三角形的性质得出对应线段之间的比值是解题关键．
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
9、如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠ABC=
如图，已知AD=BC．EC⊥AB．DF⊥AB，C．D为垂足，要使△AFD≌△BEC，还需添加一个条件．若以“ASA”为依据，则添加的条件是
如图，已知AD=BC，AC=BD，∠DAC与∠CBD有什么关系？说说你的理由．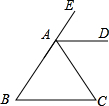
如图，已知AD∥BC，AD平分∠CAE，试说明△ABC是等腰三角形．
如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠C=