Question

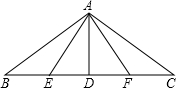
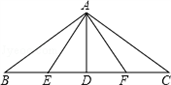
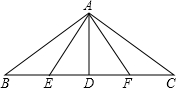如图，钢索斜拉大桥为等腰三角形，支柱高24米，∠B=∠C=30°，E、F分别为BD、CD中点，试求（精确到1米）：
（1）B、C两点之间的距离为

 

米；
（2）钢索AB的长度为

 

米；
（3）钢索AE的长度的长度为

 

米．

Answer 1

分析：根据直角三角形的性质及勾股定理解答即可．

解答：解：（1）∵大桥为等腰三角形，支柱高24米，∠B=∠C=30°，
∴AB=AC=48米，BC=2BD，再根据勾股定理求得BD=24

3

≈41.6米，
则BC=2BD≈83米；

（2）∵∠B=30°，∴AB=48米；

（3）∵E为BD的中点，∴ED=

1

2

BD=

1

2

×41.6=20.8米，
由勾股定理得AE=

AD2+ED2

=

242+20.82

≈30米．

点评：运用了直角三角形的性质及勾股定理：30°所对的直角边是斜边的一半．