题目内容
在一个不透明的袋子中装有3个红球，2个白球和4个黄球，每个球除颜色外完全相同，将球摇匀，从中任取1球，记“恰好取出红球”的概率为P（1），“恰好取出白球”的概率为P（2），“恰好取出黄球”的概率为P（3），“恰好取出不是黄球”的概率为P（4），则P（1）、P（2）、P（3）、P（4）的大、小关系是______（用“＜”号连接）．
解：因为袋子中共有9个球，其中3个红球，2个白球，4个黄球，
所以P（1）=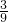
=
；
P（2）=
；
P（3）=
；
P（4）=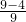
=
；
则P（2）＜P（1）＜P（3）＜P（4）．
故答案为P（2）＜P（1）＜P（3）＜P（4）．
分析：运用概率公式分别求出P（1）、P（2）、P（3）、P（4），然后比较大小，就可得到答案．
点评：本题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
所以P（1）=
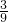=；P（2）=
；P（3）=
；P（4）=
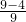=；则P（2）＜P（1）＜P（3）＜P（4）．
故答案为P（2）＜P（1）＜P（3）＜P（4）．
分析：运用概率公式分别求出P（1）、P（2）、P（3）、P（4），然后比较大小，就可得到答案．
点评：本题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目