题目内容
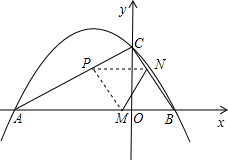
 二次函数y=ax2+bx+c的图象如图所示,则下列结论错误的是
二次函数y=ax2+bx+c的图象如图所示,则下列结论错误的是
- A.abc>0
- B.a-b+c=0
- C.a+b+c>0
- D.4a-2b+c>0
C
分析:由抛物线的开口方向向上可以得到a>0,由与y轴的交点为在y轴的负半轴上可以推出c<0,而对称轴为x=- >0可以推出b<0,由此可以确定abc的符号,再利用图象与x轴交于点(-1,0),(2,0)得出x=1,x=-1,以及x=-2时y的值即可得出答案.
>0可以推出b<0,由此可以确定abc的符号,再利用图象与x轴交于点(-1,0),(2,0)得出x=1,x=-1,以及x=-2时y的值即可得出答案.
解答:∵抛物线的开口方向向上,
∴a>0,
∵与y轴的交点为在y轴的负半轴,
∴c<0,
∵对称轴为x=- >0,
>0,
∴b<0,
∴abc>0,故此结论正确,不符合题意;
∵图象与x轴交于点(-1,0),(2,0)
∴x=-1时,y=a-b+c=0,故此结论正确,不符合题意;
当x=1时,y=a+b+c<0,故此结论错误,符合题意;
当x=-2时y=4a-2b+c>0,故此结论正确,不符合题意.
故选:C.
点评:本题考查了二次函数图象和系数的关系,注意:图象的开口方向决定a的符号,图象与y轴的交点求出c的符号,根据图象,把x=1,x=-1,以及x=-2代入y=ax2+bx+c得出各式的符号是解题关键.
分析:由抛物线的开口方向向上可以得到a>0,由与y轴的交点为在y轴的负半轴上可以推出c<0,而对称轴为x=-
 >0可以推出b<0,由此可以确定abc的符号,再利用图象与x轴交于点(-1,0),(2,0)得出x=1,x=-1,以及x=-2时y的值即可得出答案.
>0可以推出b<0,由此可以确定abc的符号,再利用图象与x轴交于点(-1,0),(2,0)得出x=1,x=-1,以及x=-2时y的值即可得出答案.解答:∵抛物线的开口方向向上,
∴a>0,
∵与y轴的交点为在y轴的负半轴,
∴c<0,
∵对称轴为x=-
 >0,
>0,∴b<0,
∴abc>0,故此结论正确,不符合题意;
∵图象与x轴交于点(-1,0),(2,0)
∴x=-1时,y=a-b+c=0,故此结论正确,不符合题意;
当x=1时,y=a+b+c<0,故此结论错误,符合题意;
当x=-2时y=4a-2b+c>0,故此结论正确,不符合题意.
故选:C.
点评:本题考查了二次函数图象和系数的关系,注意:图象的开口方向决定a的符号,图象与y轴的交点求出c的符号,根据图象,把x=1,x=-1,以及x=-2代入y=ax2+bx+c得出各式的符号是解题关键.

练习册系列答案
相关题目
 点C
点C 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是 (2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:
(2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法: