题目内容
已知一次函数y=kx+b的图象过点A(0,1)和点B(a,-3a)(a<0),且与反比例函数y=-
 的图象交于B,C两点.
的图象交于B,C两点.
(1)求a的值和一次函数的解析式;
(2)求△BOC的面积;
(3)根据图象,直接写出当x为何值时,使得一次函数的值小于反比例函数的值.
解:(1)∵点B(a,-3a)(a<0),在反比例函数y=- 的图象上,
的图象上,
∴- =-3a,
=-3a,
解得a=-1,
∴点B的坐标是(-1,3),
∴ ,
,
解得 ,
,
∴一次函数的解析式为y=-2x+1,
故答案为:a=-1,一次函数的解析式为y=-2x+1;
(2)两函数解析式联立得, ,
,
解得 ,
, ,
,
∴点C的坐标是( ,-2),
,-2),
∴S△BOC=S△AOB+S△AOC= ×|OA|×|xB|+
×|OA|×|xB|+ ×|OA|×|xC|,
×|OA|×|xC|,
= ×1×1+
×1×1+ ×1×
×1× ,
,
= +
+ ,
,
= ;
;
(3)根据图象,当-1<x<0或x> 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.
分析:(1)把点B的坐标代入反比例函数解析式求解即可得到a的值,然后利用待定系数法求解即可得到一此函数解析式;
(2)一次函数解析式与反比例函数解析式联立求解即可得到点C的坐标,然后根据S△BOC=S△AOB+S△AOC列式进行计算即可求解;
(3)找出一次函数图象在反比例函数图象下方的自变量x的取值范围即可.
点评:本题考查了一次函数与反比例函数的交点问题,待定系数法求函数解析式,根据反比例函数解析式求出a的值是解题的关键,也是本题的突破口.
 的图象上,
的图象上,∴-
 =-3a,
=-3a,解得a=-1,
∴点B的坐标是(-1,3),
∴
 ,
,解得
 ,
,∴一次函数的解析式为y=-2x+1,
故答案为:a=-1,一次函数的解析式为y=-2x+1;
(2)两函数解析式联立得,
 ,
,解得
 ,
, ,
,∴点C的坐标是(
 ,-2),
,-2),∴S△BOC=S△AOB+S△AOC=
 ×|OA|×|xB|+
×|OA|×|xB|+ ×|OA|×|xC|,
×|OA|×|xC|,=
 ×1×1+
×1×1+ ×1×
×1× ,
,=
 +
+ ,
,=
 ;
;(3)根据图象,当-1<x<0或x>
 时,一次函数的值小于反比例函数的值.
时,一次函数的值小于反比例函数的值.分析:(1)把点B的坐标代入反比例函数解析式求解即可得到a的值,然后利用待定系数法求解即可得到一此函数解析式;
(2)一次函数解析式与反比例函数解析式联立求解即可得到点C的坐标,然后根据S△BOC=S△AOB+S△AOC列式进行计算即可求解;
(3)找出一次函数图象在反比例函数图象下方的自变量x的取值范围即可.
点评:本题考查了一次函数与反比例函数的交点问题,待定系数法求函数解析式,根据反比例函数解析式求出a的值是解题的关键,也是本题的突破口.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.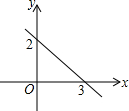 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.