题目内容
抛物线y=（1+x）（3-x）
- A.有最大值3
- B.有最小值-3
- C.有最大值4
- D.有最小值4
C
分析：将抛物线解析式转化为一般式，再配方，求出函数的最值．
解答：∵y=（1+x）（3-x）
=-x2+2x+3
=-（x2-2x）+3
=-（x2-2x+1-1）+3
=-（x2-2x+1）+4
=-（x-1）2+4，
∴抛物线有最大值4．
故选C．
点评：本题考查了二次函数的最值，根据二次项系数判断出函数有最大值还是最小值，再利用配方法是解答此类问题的基本思路．
分析：将抛物线解析式转化为一般式，再配方，求出函数的最值．
解答：∵y=（1+x）（3-x）
=-x2+2x+3
=-（x2-2x）+3
=-（x2-2x+1-1）+3
=-（x2-2x+1）+4
=-（x-1）2+4，
∴抛物线有最大值4．
故选C．
点评：本题考查了二次函数的最值，根据二次项系数判断出函数有最大值还是最小值，再利用配方法是解答此类问题的基本思路．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
A和C，和x轴的另一个交点为B．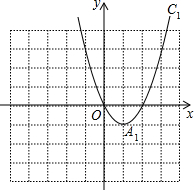
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．