题目内容
 锐角三角ABC的三边是a,b,c,它的外心到三边的距离分别为m,n,p,那么m:n:p等于
锐角三角ABC的三边是a,b,c,它的外心到三边的距离分别为m,n,p,那么m:n:p等于
- A.
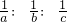
- B.a:b:c
- C.cosA:cosB:cosC
- D.sinA:sinB:sinC
C
分析:根据外心的性质可知,OA=OB=OC,在Rt△COD中,∠COD= ∠COB=∠A,故OC=
∠COB=∠A,故OC= =
= ,同理可得OB=
,同理可得OB= ,OA=
,OA= ,代入OA=OB=OC中求解.
,代入OA=OB=OC中求解.
解答: 解:如图⊙O经过A、B、C三点,连接OA、OB、OC,
解:如图⊙O经过A、B、C三点,连接OA、OB、OC,
则OA=OB=OC,
在Rt△COD中,∵∠COD= ∠COB=∠A,∴OC=
∠COB=∠A,∴OC= =
= ,
,
同理可得OB= ,OA=
,OA= ,
,
∴ =
= =
= ,
,
即m:n:p=cosA:cosB:cosC.
故选C.
点评:本题考查的是三角形外心的性质.重点在于理解圆周角与圆心角的关系,解直角三角形的知识.
分析:根据外心的性质可知,OA=OB=OC,在Rt△COD中,∠COD=
 ∠COB=∠A,故OC=
∠COB=∠A,故OC= =
= ,同理可得OB=
,同理可得OB= ,OA=
,OA= ,代入OA=OB=OC中求解.
,代入OA=OB=OC中求解.解答:
 解:如图⊙O经过A、B、C三点,连接OA、OB、OC,
解:如图⊙O经过A、B、C三点,连接OA、OB、OC,则OA=OB=OC,
在Rt△COD中,∵∠COD=
 ∠COB=∠A,∴OC=
∠COB=∠A,∴OC= =
= ,
,同理可得OB=
 ,OA=
,OA= ,
,∴
 =
= =
= ,
,即m:n:p=cosA:cosB:cosC.
故选C.
点评:本题考查的是三角形外心的性质.重点在于理解圆周角与圆心角的关系,解直角三角形的知识.

练习册系列答案
相关题目