题目内容
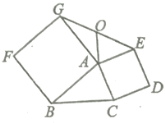
【题目】如图,分别以![]() 的边向外作正方形ABFG和ACDE,连接EG,若O为EG的中点,
的边向外作正方形ABFG和ACDE,连接EG,若O为EG的中点,
求证:(1)![]() ;
;
(2)![]() .
.
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)如图,延长AO到M,使OM=AO,连接GM,延长OA交BC于点H.根据全等三角形的性质得到AE=MG,∠MGO=∠AEO,根据三角形的内角和得到∠MGA+∠GAE=180°,根据正方形的性质得到AG=AB,AE=AC,∠BAG=∠CAE=90°,根据全等三角形的性质得到AM=BC,等量代换即可得到结论;
(2)根据全等三角形的性质得到∠M=∠EAO,∠M=∠ACB,等量代换得到∠EAO=∠ACB,求得∠AHC=90°,根据垂直的定义即可得到结论.
解:(1)如图,延长AO到M,使OM=AO,连接GM,延长OA交BC于点H.

∵O为EG的中点,
∴OG=OE,
在△AOE与△MOG中,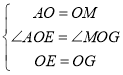 ,
,
∴△AOE≌△MOG(SAS),
∴AE=MG,∠MGO=∠AEO,
∴∠MGA+∠GAE=180°,
∵四边形ABFG和四边形ACDE是正方形,
∴AG=AB,AE=AC,∠BAG=∠CAE=90°,
∴AC=GM,∠GAE+∠BAC=180°,
∴∠BAC=∠AGM,
在△AGM与△ABC中,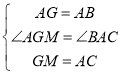 ,
,
∴△AGM≌△ABC(SAS),
∴AM=BC,
∵AM=2AO,
∴![]() ;
;
(2)由(1)知,△AOE≌△MOG,△AGM≌△ABC,
∴∠M=∠EAO,∠M=∠ACB,
∴∠EAO=∠ACB,
∵∠CAE=90°,
∴∠OAE=∠CAH=90°,
∴∠ACB+∠CAH=90°,
∴∠AHC=90°,
∴AH⊥BC.
即![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目