题目内容
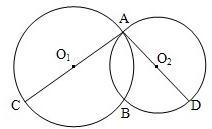
如图，已知⊙O1、⊙O2相交于A、B两点，且点O1在⊙O2上，过A作⊙O1的切线AC交BO1的延长线于点P，交⊙O2于点C，BP交⊙O1于点D，若PD=1，PA=
，则AC的长为
- A.
- B.
- C.
- D.
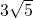
B
分析：根据PA2=PD•PB，作为相等关系可求得PB=5，BD=4，O1D=O1B=2，再根据割线定理PA•PC=PO1•PB，可求得PC=3，
从而求得AC=2．
解答：∵PA2=PD•PB，即（）2=1×PB，
解得PB=5，
∴BD=BP-PD=5-1=4，O1D=O1B=4÷2=2，
∵PA•PC=PO1•PB，
∴×PC=3×5，
即PC=3，
∴AC=PC-AP=3-=2．
故选B．
点评：根据切割线定理和割线定理解答．此题要关注两个关键点：A为两圆交点，PB过点O1．
分析：根据PA2=PD•PB，作为相等关系可求得PB=5，BD=4，O1D=O1B=2，再根据割线定理PA•PC=PO1•PB，可求得PC=3
，从而求得AC=2
．解答：∵PA2=PD•PB，即（
）2=1×PB，解得PB=5，
∴BD=BP-PD=5-1=4，O1D=O1B=4÷2=2，
∵PA•PC=PO1•PB，
∴
×PC=3×5，即PC=3
，∴AC=PC-AP=3
-=2．故选B．
点评：根据切割线定理和割线定理解答．此题要关注两个关键点：A为两圆交点，PB过点O1．
练习册系列答案
相关题目
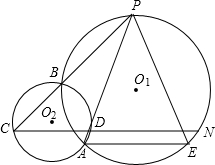
25、如图，已知⊙O1和⊙O2相交于A、B，AC、AD分别是两圆的直径，
如图：已知⊙O1和⊙O2相交于A、B两点，P是⊙O1上一点，PB的延长线交⊙O2于点C，PA交⊙O2于点D，CD的延长线交⊙O1于点N．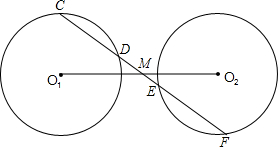
助线或另添字母），则M是线段O1O2的中点，并说明理由．（说明理由时可添加辅助线或字母）
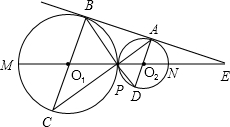长线交⊙O1于C点，BP的延长线交⊙O2于D点，直线O1O2交⊙O1于M，交⊙O2于N，与BA的延长线交于点E．