题目内容
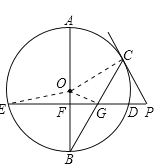
【题目】(10分)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.

(1)求证:PC=PG;
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为![]() 时,求弦ED的长.
时,求弦ED的长.
【答案】(1)详见解析;(2)详见解析;(3)DE=4![]() .
.
【解析】
试题分析:(1)连结OC,根据切线的性质得OC⊥PC,可得∠OCG+∠PCG=90°,由ED⊥AB得∠B+∠BGF=90°,又因∠B=∠OCG,所以∠PCG=∠BGF,根据对顶角相等得∠BGF=∠PGC,
于是∠PGC=∠PCG,所以PC=PG;
(2)连结OG,由点G是BC的中点,根据垂径定理的推论得OG⊥BC,BG=CG,易证得Rt△BOG∽Rt△BGF,则BG:BF=BO:BG,即BG2=BOBF,把BG用CG代换得到CG2=BOBF;
(3)连结OE,OG=OG=![]() ,在Rt△OBG中,利用勾股定理计算出BG的长,再利用BG2=BOBF可计算出BF,从而得到OF=1的长,在Rt△OEF中,根据勾股定理计算出EF的长,由于AB⊥ED,根据垂径定理可得EF=DF,再根据DE=2EF即可得DE的长.
,在Rt△OBG中,利用勾股定理计算出BG的长,再利用BG2=BOBF可计算出BF,从而得到OF=1的长,在Rt△OEF中,根据勾股定理计算出EF的长,由于AB⊥ED,根据垂径定理可得EF=DF,再根据DE=2EF即可得DE的长.
试题解析:(1)证明:连结OC,如图,
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠OCG+∠PCG=90°,
∵ED⊥AB,
∴∠B+∠BGF=90°,
∵OB=OC,
∴∠B=∠OCG,
∴∠PCG=∠BGF,
而∠BGF=∠PGC,
∴∠PGC=∠PCG,
∴PC=PG;
(2)解:CG、BF、BO三者之间的数量关系为CG2=BOBF.理由如下:
连结OG,如图,
∵点G是BC的中点,
∴OG⊥BC,BG=CG,
∴∠OGB=90°,
∵∠OBG=∠GBF,
∴Rt△BOG∽Rt△BGF,
∴BG:BF=BO:BG,
∴BG2=BOBF,
∴CG2=BOBF;
(3)解:连结OE,如图,
由(2)得OG⊥BC,
∴OG=![]() ,
,
在Rt△OBG中,OB=5,
∴BG=![]() =2
=2![]() ,
,
由(2)得BG2=BOBF,
∴BF=![]() =4,
=4,
∴OF=1,
在Rt△OEF中,EF=![]() =2
=2![]() ,
,
∵AB⊥ED,
∴EF=DF,
∴DE=2EF=4![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案