题目内容
 如图,点C在反比例函数y=
如图,点C在反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)将过点O且与OC所在直线关于y轴对称的直线向上平移2个单位后得到直线AB,如果CD=1,求直线AB的解析式.
分析:(1)在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
,且保持不变,再根据反比例函数的图象所在的象限确定k的值,即可求出反比例函数的解析式.
(2)由已知条件易得C的坐标,根据对称可求得C关于y轴对称的点的坐标,从而求得OC所在直线关于y轴对称的直线的解析式,根据平移k不变,b值加减即可得出答案.
| |k| |
| 2 |
(2)由已知条件易得C的坐标,根据对称可求得C关于y轴对称的点的坐标,从而求得OC所在直线关于y轴对称的直线的解析式,根据平移k不变,b值加减即可得出答案.
解答:解:(1)∵△ODC的面积是3,
∴OD•DC=6
∵点C在y=
的图象上,
∴xy=k.(1分)
∴(-y)x=6,
∴k=xy=-6.
∴所求反比例函数解析式为y=-
.(2分)
(2)∵CD=1,即点C(1,y),
把x=1代入y=-
,得y=-6.
∴C(1,-6).
∴C点关于y轴对称点为C′(-1,-6).
∴过点O且与OC所在直线关于y轴对称的直线为y=6x.
∴将直线y=6x向上平移2个单位后得到直线AB的解析式为y=6x+2.
∴OD•DC=6
∵点C在y=
| k |
| x |
∴xy=k.(1分)
∴(-y)x=6,
∴k=xy=-6.
∴所求反比例函数解析式为y=-
| 6 |
| x |
(2)∵CD=1,即点C(1,y),
把x=1代入y=-
| 6 |
| x |
∴C(1,-6).
∴C点关于y轴对称点为C′(-1,-6).
∴过点O且与OC所在直线关于y轴对称的直线为y=6x.
∴将直线y=6x向上平移2个单位后得到直线AB的解析式为y=6x+2.
点评:本题综合考查了反比例函数.用到的知识点为:待定系数法求函数解析式,反比例函数图象和性质,及上下平移直线解析式只改变常数项,上加,下减;左右平移不改变直线解析式中的k,关键是得到平移后经过的一个具体点;求关于某条直线对称的直线解析式,难点是得到新直线解析式上的2个具体点.

练习册系列答案
相关题目
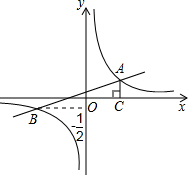 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0).
的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0). 上,求点D1的坐标;
上,求点D1的坐标;
 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.
,过点A作AC⊥x轴于点C,AC=1,OC=2. (x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.
(x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.