题目内容
二次函数 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:

(1)写出方程 的两个根.
的两个根.
(2)写出不等式 的解集.
的解集.
(3)写出 随
随 的增大而减小的自变量
的增大而减小的自变量 的取值范围.
的取值范围.
(4)若方程 有两个不相等的实数根,求
有两个不相等的实数根,求 的取值范围.
的取值范围.
【答案】
(1) x1=1,x2=3;(2) 1<x<3;(3)x>2;(4)k<2.
【解析】
试题分析:(1)看与x轴的交点即可;
(2)看y轴上方的函数图象相对应的x的值即可;
(3)看对称轴右侧的函数图象相对应的x的范围即可;
(4)先移项,整理为一元二次方程,让根的判别式大于0求值即可.
试题解析:(1)∵二次函数y=ax2+bx+c的图象与x轴的交点为(1,0),(3,0)
∴方程ax2+bx+c=0的两个根x1=1,x2=3;
(2)由二次函数y=ax2+bx+c的图象可知:1<x<3时,二次函数y=ax2+bx+c的值大于0
∴不等式ax2+bx+c>0的解集为1<x<3;
(3)由图象可知:二次函数y=ax2+bx+c的对称轴为x=2
∴y随x的增大而减小的自变量x的取值范围为x>2;
(4)由图象可知:二次函数y=ax2+bx+c的顶点坐标为(2,2),
当直线y=k,在(0,2)的下边时,一定与抛物线有两个不同的交点,因而当k<2时,方程ax2+bx+c=k有两个不相等的实数根.
考点: 1.抛物线与x轴的交点;2.二次函数与不等式(组).

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
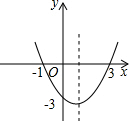 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
已知二次函数的图象如图所示,则这个二次函数的表达式为( )| A、y=x2-2x+3 | B、y=x2-2x-3 | C、y=x2+2x-3 | D、y=x2+2x+3 |
 16、已知二次函数的图象如图所示,则
16、已知二次函数的图象如图所示,则 21、已知二次函数的图象如图所示,求它的解析式.
21、已知二次函数的图象如图所示,求它的解析式. 二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点.
二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点. 二次函数的图象如图所示,则a
二次函数的图象如图所示,则a