Question

如图，已知AB是⊙O的直径，C、D为⊙O上两点，CF⊥AB于点F，CE⊥AD的延长线于点E，且 CE＝CF．

（1）求证：CE是⊙O的切线；

（2）若AD＝CD＝6，求四边形ABCD的面积．

Answer 1

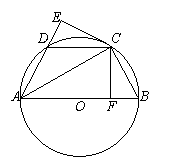
证明：（1）连结OC.

∵CF⊥AB ，CE⊥AD，且CE=CF

∴∠CAE=∠CAB                        

∵ OC=OA

∴ ∠CAB＝∠OCA

∴∠CAE＝∠OCA                       

     ∴∠OCA＋∠ECA＝∠CAE＋∠ECA＝90°   

     又∵OC是⊙O的半径

     ∴CE是⊙O的切线                        、

（2）∵AD=CD

∴∠DAC=∠DCA=∠CAB

∴DC//AB                                  

∵∠CAE＝∠OCA

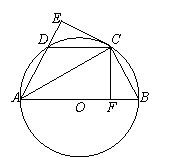∴OC//AD

∴四边形AOCD是平行四边形              

∴OC=AD=6，AB＝12                       ………

∵∠CAE=∠CAB

∴弧CD=弧CB

∴CD=CB＝6

∴△OCB是等边三角形                      ………

∴                              

∴S_{四边形ABCD}＝