题目内容
平面直角坐标系中，点A的坐标是（4，0），点P在直线y=﹣x+m上，且AP=OP=4．求m的值．
| 解：由已知AP=OP，点P在线段OA的垂直平分线PM上． ∴OA=AP=OP=4， ∴△AOP是等边三角形． 如图，当点P在第一象限时，OM=2，OP=4． 在Rt△OPM中， PM=  ，∴P（2，  ）．∵点P在y=﹣x+m上， ∴m=2+  ．当点P在第四象限时，根据对称性，P'（（2，﹣  ）．∵点P'在y=﹣x+m上， ∴m=2﹣  ．则m的值为2+  或2﹣ ． |
 |
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
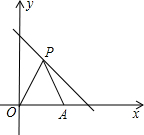如图，在平面直角坐标系中，点P（x，y）是第一象限直线y=-x+6上的点，点A坐标是（5，0），O是坐标原点，△PAO的面积为m，则m关于x的函数关系式是
如图，在平面直角坐标系中，点A是抛物线y=a（x+2）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为（ ）