题目内容
如图，已知AB∥CD，若∠A=20°，∠E=35°，求∠C．
解：∵∠A=20°，∠E=35°，
∴∠EFB=∠A+∠E=55°，
∵AB∥CD，
∴∠C=∠EFB=55°．
分析：根据三角形的外角等于和它不相邻的两个内角的和以及平行线的性质进行求解．
点评：此题考查了三角形的外角的性质以及平行线的性质．三角形的外角等于和它不相邻的两个内角的和；两条直线平行，则同位角相等．
∴∠EFB=∠A+∠E=55°，
∵AB∥CD，
∴∠C=∠EFB=55°．
分析：根据三角形的外角等于和它不相邻的两个内角的和以及平行线的性质进行求解．
点评：此题考查了三角形的外角的性质以及平行线的性质．三角形的外角等于和它不相邻的两个内角的和；两条直线平行，则同位角相等．
练习册系列答案
相关题目
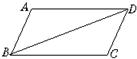15、如图，已知AB=CD且∠ABD=∠BDC，要证∠A=∠C，判定△ABD≌△CDB的方法是（ ）
如图，已知AB∥CD，∠1=50°25′，则∠2的大小是
如图，已知 AB∥CD，∠A=53°，则∠1的度数是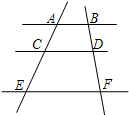
如图，已知AB∥CD∥EF，那么下列结论中，正确的是（ ）