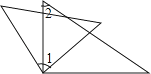
题目内容
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC.
(1)求证:AC是⊙O的切线;
(2)若BD=OB=4,求弦AE的长.
【答案】
(1)
证明:连接OE,
∵CD与圆O相切,
∴OE⊥CD,
∴∠CEO=90°,
∵BE∥OC,
∴∠AOC=∠OBE,∠COE=∠OEB,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠AOC=∠COE,
在△AOC和△EOC中,
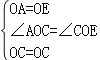 ,
,
∴△AOC≌△EOC(SAS),
∴∠CAO=∠CEO=90°,
则AC与圆O相切;
(2)
解:在Rt△DEO中,BD=OB,
∴BE=![]() OD=OB=4,
OD=OB=4,
∵OB=OE,
∴△BOE为等边三角形,
∴∠ABE=60°,
∵AB为圆O的直径,
∴∠AEB=90°,
∴AE=BEtan60°=![]()
【解析】(1)连接OE,根据CD与圆O相切,利用切线的性质得到OE垂直于CD,再由OC与BE平行,得到同位角相等与内错角相等,根据OB=OE,利用等边对等角得到一对角相等,等量代换得到夹角相等,再由OA=OE,OC=OC,利用SAS得到三角形AOC与三角形EOC全等,利用全等三角形对应角相等得到∠OAC=∠OEC=90°,即可得证;
(2)根据题意得到EB为直角三角形斜边上的中线,求出EB的长,再由OE=OB=EB得到三角形OEB为等边三角形,求出∠ABE=60°,根据AB为圆O直径,利用直径所对的圆周角为直角得到三角形AEB为直角三角形,利用锐角三角函数定义求出AE的长即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目