Question

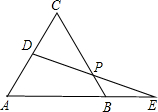
已知：如图，正△ABC的边长为a，D为AC边上的一个动点，延长AB至E，使BE=CD，连接DE，

交BC于点P．
（1）求证：DP=PE；
（2）若D为AC的中点，求BP的长．

Answer 1

（1）证明：过点D作DF∥AB，交BC于F．
∵△ABC为正三角形，
∴∠CDF=∠A=60°．
∴△CDF为正三角形．
∴DF=CD．
又BE=CD，
∴BE=DF．
又DF∥AB，
∴∠PEB=∠PDF．
∵在△DFP和△EBP中，
∵

∠BPE=∠FPD ∠PEB=∠PDF BE=FD

，
∴△DFP≌△EBP（AAS）．
∴DP=PE．

（2）由（1）得△DFP≌△EBP，可得FP=BP．
∵D为AC中点，DF∥AB，
∴BF=

1

2

BC=

1

2

a．
∴BP=

1

2

BF=

1

4

a．