Question

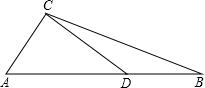如图在△ABC中，点D是AB的中点，DC⊥AC，且tan∠BCD=

1

3

．求∠A的四个三角函数值．

Answer 1

分析：如图，过点D作DE∥AC交BC于E，设出DE边的长，则在Rt△ACD中，各边的长均可用CD的边表示出来，代入∠A的三角函数值可求得．

解答：解：如图过点D作DE∥AC交BC于E，又由DC⊥AC，可得∠ACD=∠CDE=90°，
设DE=x，由tan∠BCD=

DE

CD

=

1

3

，
可得：CD=3x，
∵DE∥AC，D是AB的中点，
∴

DE

AC

=

DB

AB

=

1

2

，
∴AC=2x，
在Rt△ACD中，AD=

AC2+CD2

=

(3x)2+(2x)2

=

13

x，
故sinA=

CD

AD

=

3

13

13

；
cosA=

AC

AD

=

2

13

13

；
tanA=

CD

AC

=

3

2

；
cotA=

AC

CD

=

2

3

．

点评：本题主要要求掌握三角函数的求法，同时对于三角函数的定义式也要求很熟悉．