题目内容
抛物线y=x2-4x+3与x轴交于A、B，与y轴交于C，则△ABC的面积=________．
1
分析：y=0时可求出A、B两点的坐标，则可得线段AB的长，再求出顶点C的纵坐标．即可求出△ABC的面积．
解答：y=0时，0=x2-4x+3，
解得x1=3，x2=1
∴线段AB的长为2，
∵顶点C的纵坐
=-1，
∴以AB为底的△ABC的高为1，
∴S△ABC=
×2×1=1，
故答案为：1．
点评：此题主要考查了二次函数与坐标轴的交点坐标求法，进而得出有关三角形的面积，正确的得出有关点的坐标是解决问题的关键．
分析：y=0时可求出A、B两点的坐标，则可得线段AB的长，再求出顶点C的纵坐标．即可求出△ABC的面积．
解答：y=0时，0=x2-4x+3，
解得x1=3，x2=1
∴线段AB的长为2，
∵顶点C的纵坐
=-1，∴以AB为底的△ABC的高为1，
∴S△ABC=
×2×1=1，故答案为：1．
点评：此题主要考查了二次函数与坐标轴的交点坐标求法，进而得出有关三角形的面积，正确的得出有关点的坐标是解决问题的关键．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
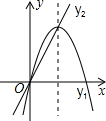如图，抛物线y1=-x2+4x和直线y2=2x．当y1＞y2时，x的取值范围是（ ）| A、0＜x＜2 | B、x＜0或x＞2 | C、x＜0或x＞4 | D、0＜x＜4 |