题目内容
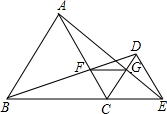 如图,△ABC与△DCE都是等边三角形,且点B、C、E在同一条直线上,
如图,△ABC与△DCE都是等边三角形,且点B、C、E在同一条直线上,(1)试问AE与BD的大小关系,并对你所得的结论说明理由.
(2)试问AG与BF的大小关系,并对你所得的结论说明理由.
(3)试问FG与BE有何位置关系,并对你所得的结论说明理由.
分析:(1)利用等边三角形的性质证明△BCD≌△ACE就可以得出结论;
(2)利用(1)的结论证明△BFC≌△AGC就可以得出结论;
(3)由(2)的克伦可以得出CF=CG,就可以求出∠FGC=60°,从而得出结论FG∥BE.
(2)利用(1)的结论证明△BFC≌△AGC就可以得出结论;
(3)由(2)的克伦可以得出CF=CG,就可以求出∠FGC=60°,从而得出结论FG∥BE.
解答:(1)AE=BD.
证明:∵△ABC与△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∵∠ACB+∠ACD++∠DCE=180,
∴∠ACD=60°,∠ACB+∠ACD=∠ACD+∠DCE,
即∠BCD=∠ACE.
在△BCD和△ACE中,
∵
,
∴△BCD≌△ACE,
∴AE=BD
(2)AG=BF,
证明:∵△BCD≌△ACE,
∴∠CBD=∠CAE.
在△BCF和△ACG中
,
∴△BCF≌△ACG,
∴BF=AG.
(3)FG∥BE,
证明:∵△BCE≌△ACG,
∴CF=CG.
∵∠ACD=60°,
∴△CFG为等边三角形,
∴∠CGF=60°,
∴∠CGF=∠DCE,
∴FG∥BE.
证明:∵△ABC与△DCE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°.
∵∠ACB+∠ACD++∠DCE=180,
∴∠ACD=60°,∠ACB+∠ACD=∠ACD+∠DCE,
即∠BCD=∠ACE.
在△BCD和△ACE中,
∵
|
∴△BCD≌△ACE,
∴AE=BD
(2)AG=BF,
证明:∵△BCD≌△ACE,
∴∠CBD=∠CAE.
在△BCF和△ACG中
|
∴△BCF≌△ACG,
∴BF=AG.
(3)FG∥BE,
证明:∵△BCE≌△ACG,
∴CF=CG.
∵∠ACD=60°,
∴△CFG为等边三角形,
∴∠CGF=60°,
∴∠CGF=∠DCE,
∴FG∥BE.
点评:本题考查了等边三角形的性质的运用及全等三角形的判定和性质的运用.解答中运用全等解决线段的相等和平行是关键.

练习册系列答案
相关题目
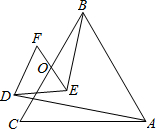 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
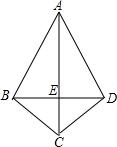 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.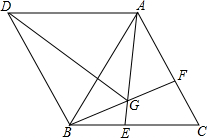 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G. 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.