��Ŀ����
����Ŀ�����꼶�߰�����ѧ��ȤС�����Ժ����ĶԳƱ任����̽����������̽���������ù��̣��벹��������
(1)��������
��������y��|x|��ͼ��ʱ�������˷ֶκ����İ취���ú���ת��Ϊy��![]() ,������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ����
,������ͼ1��ʾ��ƽ��ֱ������ϵ������������ͼ����
(2)���̽��
������y��|x��1|��ͼ����ת��Ϊ�ֶκ���y��![]() ��Ȼ��ֱ��������κ�����ͼ������С���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y��x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y��|x��1|��ͼ����ͼ2��ʾ��
��Ȼ��ֱ��������κ�����ͼ������С���������ƽ���ϵ���Գ�֪ʶ���Ѻ���y��x��1��x�����沿�֣���x����з��ۣ���x���ϼ����沿������˺���y��|x��1|��ͼ����ͼ2��ʾ��
(3)��չ���
��ͼ3�Ǻ���y��x2��2x��3��ͼ������ԭƽ��ֱ������ϵ������y��|x2��2x��3|��ͼ����
(4)ʵ������
�ٺ���y��|x2��2x��3|��ͼ����x���� �����㣬��Ӧ����|x2��2x��3|��0�� ��ʵ����
�ں���y��|x2��2x��3|��ͼ����ֱ��y��5�� �����㣬��Ӧ����|x2��2x��3|��5�� ��ʵ����
�ۺ���y��|x2��2x��3|��ͼ����ֱ��y��4�� �����㣬��Ӧ����|x2��2x��3|��4�� ��ʵ����
�ܹ���x�ķ���|x2��2x��3|��a��4��ʵ��ʱ��a��ȡֵ��Χ�� ��

���𰸡�(1)��ͼ�������� (3) ��ͼ������;
(4)��2��2����2��2����3,3����0��a��4��
����������������� ![]() ������㷨��
������㷨��![]() ��ͼ��
��ͼ��
![]() ���ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�����
���ݾ���ֵ�����壬���÷������۵�˼��д���ֶκ�����
![]() ��
��![]() ������ͼ��ķ���һ�����Ѻ���
������ͼ��ķ���һ�����Ѻ���![]() ��ͼ����
��ͼ����![]() �����沿�֣���
�����沿�֣���![]() ����з��ۿɵõ�����
����з��ۿɵõ�����![]() ��ͼ��
��ͼ��
![]() ���û�����ͼ��ͨ��ȷ��
���û�����ͼ��ͨ��ȷ��![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() �Ľ������������⣮
�Ľ������������⣮
��������� ![]() ����������ͼ
����������ͼ![]() ��
��
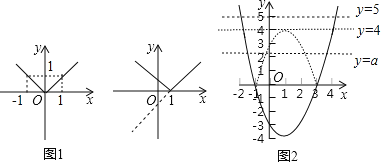
![]() ���̽��
���̽��
������![]() ��ͼ��,����ת��Ϊ�ֶκ���
��ͼ��,����ת��Ϊ�ֶκ���![]()
![]() ��չ���
��չ���
�Ѻ���![]() ��ͼ����
��ͼ����![]() �����沿�֣���
�����沿�֣���![]() ����з��ۿɵõ�������ͼ��
����з��ۿɵõ�������ͼ��
��![]() ���ϼ����沿������˺���
���ϼ����沿������˺���![]() ��ͼ����ͼ
��ͼ����ͼ![]() ��
��
![]() �ٺ���
�ٺ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ں���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��
��![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ۺ���![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��
��![]() ������,��Ӧ����
������,��Ӧ����![]() ��
��![]() ��ʵ����
��ʵ����
�ܹ���![]() �ķ���
�ķ���![]() ��
��![]() ��ʵ��ʱ��
��ʵ��ʱ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]()
�ʴ�Ϊ�� ![]()

 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д�