题目内容
已知抛物线y=ax2+bx+c与y轴交于点A(0,3),与x轴交于(1,0)(5,0)两点,若一个动点P自OA的中点M出发,先到达x轴上的某点E,再到达抛物线的对称轴上某点F,最后运动到点A,则使点P运动的总路径最短的点E、点F的坐标分别是:E________,F________.
(2,0) (3, )
)
分析:作出草图,根据抛物线与x轴的交点求出对称轴为直线x=3,再求出点A关于对称轴的对称点A′,点M关于x轴的对称点M′,连接A′M′,根据轴对称确定最短路线问题,A′M′的长度为点P运动的总路径最短长度,然后利用待定系数法求出直线A′M′的解析式,令y=0求出点E的坐标,令x=3求出点F的坐标即可.
解答: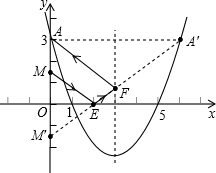 解:如图,∵抛物线与x轴交于(1,0)(5,0)两点,
解:如图,∵抛物线与x轴交于(1,0)(5,0)两点,
∴抛物线的对称轴为直线x=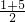 =3,
=3,
∴点A(0,3)关于直线x=3的对称点A′为(6,3),
又∵OA的中点M为(0, ),
),
∴点M关于x轴的对称点M′为(0,- ),
),
连接A′M′与x轴的交点、与对称轴的交点即为所求的点E、F,
设直线A′M′的解析式为y=kx+b,
则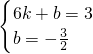 ,
,
解得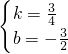 ,
,
所以,直线A′M′的解析式为y= x-
x- ,
,
令y=0,则 x-
x- =0,
=0,
解得x=2,
令x=3,则y= ×3-
×3- =
= ,
,
所以,点E(2,0),F(3, ).
).
故答案为:E(2,0);(3, ).
).
点评:本题是二次函数综合题型,主要考查了抛物线的对称性,利用轴对称确定最短路线问题,找出点A、M的对称点,确定出总路径最短时的点E、F的位置是解题的关键,作出图形更形象直观.
 )
)分析:作出草图,根据抛物线与x轴的交点求出对称轴为直线x=3,再求出点A关于对称轴的对称点A′,点M关于x轴的对称点M′,连接A′M′,根据轴对称确定最短路线问题,A′M′的长度为点P运动的总路径最短长度,然后利用待定系数法求出直线A′M′的解析式,令y=0求出点E的坐标,令x=3求出点F的坐标即可.
解答:
 解:如图,∵抛物线与x轴交于(1,0)(5,0)两点,
解:如图,∵抛物线与x轴交于(1,0)(5,0)两点,∴抛物线的对称轴为直线x=
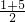 =3,
=3,∴点A(0,3)关于直线x=3的对称点A′为(6,3),
又∵OA的中点M为(0,
 ),
),∴点M关于x轴的对称点M′为(0,-
 ),
),连接A′M′与x轴的交点、与对称轴的交点即为所求的点E、F,
设直线A′M′的解析式为y=kx+b,
则
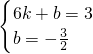 ,
,解得
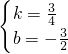 ,
,所以,直线A′M′的解析式为y=
 x-
x- ,
,令y=0,则
 x-
x- =0,
=0,解得x=2,
令x=3,则y=
 ×3-
×3- =
= ,
,所以,点E(2,0),F(3,
 ).
).故答案为:E(2,0);(3,
 ).
).点评:本题是二次函数综合题型,主要考查了抛物线的对称性,利用轴对称确定最短路线问题,找出点A、M的对称点,确定出总路径最短时的点E、F的位置是解题的关键,作出图形更形象直观.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=