题目内容
【题目】如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC,若∠BAC和∠BOC互补,则弦BC的长度为 . 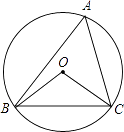
【答案】4 ![]()
【解析】解:过点O作OD⊥BC于D,
则BC=2BD,
∵△ABC内接于⊙O,∠BAC与∠BOC互补,
∴∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°,
∵OB=OC,
∴∠OBC=∠OCB= ![]() (180°﹣∠BOC)=30°,
(180°﹣∠BOC)=30°,
∵⊙O的半径为4,
∴BD=OBcos∠OBC=4× ![]() =2
=2 ![]() ,
,
∴BC=4 ![]() .
.
所以答案是:4 ![]() .
.

【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对三角形的外接圆与外心的理解,了解过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】将正整数![]() 至
至![]() 按照一定规律排成下表:
按照一定规律排成下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…… |
记![]() 表示第
表示第![]() 行第
行第![]() 个数,如
个数,如![]() 表示第
表示第![]() 行第
行第![]() 个数是
个数是![]() .
.
(1)直接写出![]() _______________,
_______________,![]() _______________;
_______________;
(2)①如果![]() ,那么
,那么![]() _________________,
_________________,![]() ________;②用
________;②用![]() ,
,![]() 表示
表示![]() __________;
__________;
(3)将表格中的![]() 个阴影格子看成一个整体并平移,所覆盖的
个阴影格子看成一个整体并平移,所覆盖的![]() 个数之和能否等于
个数之和能否等于![]() .若能,求出这
.若能,求出这![]() 个数中的最小数,若不能说明理由.
个数中的最小数,若不能说明理由.