题目内容
 如图,?ABCD中,CE=DF,则四边形ABEF是
如图,?ABCD中,CE=DF,则四边形ABEF是平行四边形
平行四边形
.分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明AF=BE,进而可以根据有一组对边平行且相等的四边形是平行四边形判定出四边形ABEF是平行四边形.
解答:解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵CE=DF,
∴AD-FD=BC-EC,
即AF=BE,
∴四边形ABEF是平行四边形.
故答案为:平行四边形.
∴AD=BC,AD∥BC,
∵CE=DF,
∴AD-FD=BC-EC,
即AF=BE,
∴四边形ABEF是平行四边形.
故答案为:平行四边形.
点评:此题主要考查了平行四边形的判定与性质,关键是掌握平行四边形对边平行且相等,一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
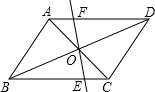 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
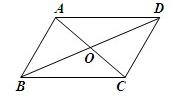 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )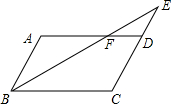 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=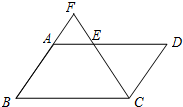 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为