题目内容
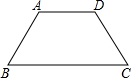 如图,等腰梯形ABCD中,AD∥BC,若AB=AD=4,BC=8,以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外,则半径r的范围是________.
如图,等腰梯形ABCD中,AD∥BC,若AB=AD=4,BC=8,以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外,则半径r的范围是________.
4<r<4
分析:利用锐角三角函数关系以及等腰三角形的性质得出∠BAC=90°,再利用勾股定理求出AC的长,即可得出r的取值范围.
解答: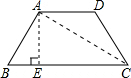 解:连接AC作AE⊥BC于点E,
解:连接AC作AE⊥BC于点E,
∵等腰梯形ABCD中,AD∥BC,AB=AD=4,BC=8,
∴BE=2,
∴cos∠B= =
= ,
,
∴∠B=60°,
∴∠BCD=60°,
∴∠BAD=∠D=120°,
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴AC=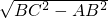 =
= =4
=4 ,
,
当以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外时,
半径r的范围是:4<r<4 ;
;
故答案为:4<r<4 .
.
点评:此题主要考查了点与圆的位置关系以及等腰梯形的性质和勾股定理等知识,利用已知得出AC的长是解题关键.

分析:利用锐角三角函数关系以及等腰三角形的性质得出∠BAC=90°,再利用勾股定理求出AC的长,即可得出r的取值范围.
解答:
 解:连接AC作AE⊥BC于点E,
解:连接AC作AE⊥BC于点E,∵等腰梯形ABCD中,AD∥BC,AB=AD=4,BC=8,
∴BE=2,
∴cos∠B=
 =
= ,
,∴∠B=60°,
∴∠BCD=60°,
∴∠BAD=∠D=120°,
∴∠DAC=∠DCA=30°,
∴∠ACB=30°,
∴∠BAC=90°,
∴AC=
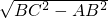 =
= =4
=4 ,
,当以点A为圆心,r为半径画圆,梯形的四个顶点只有一个在⊙A外时,
半径r的范围是:4<r<4
 ;
;故答案为:4<r<4
 .
.点评:此题主要考查了点与圆的位置关系以及等腰梯形的性质和勾股定理等知识,利用已知得出AC的长是解题关键.

练习册系列答案
相关题目
 14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( )
14、如图,等腰梯形ABCD中,AB∥CD,∠A=60°,BD平分∠ABC,若梯形ABCD的周长为40cm,则CD的长为( ) 24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC. (2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=
(2007•昌平区二模)已知:如图,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD= 如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm. 如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延长BC到E,使CE=AD.