Question

如图，∠ABC=30°，BC=4，D是BC边的中点，E是边BA上一动点，则EC+ED的最小值是________．

Answer 1

分析：作出D关于AB的对称点D′，连接CD′交AB于点E，EC+ED的最小值即为CD′的长，判断出△BCD′的形状即可得到EC+ED的最小值．
解答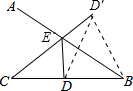：作出D关于AB的对称点D′，连接CD′交AB于点E，
由轴对称可得DB=D′B=2
∠DBA=∠D′BA=30°
∴△DD′B为等边三角形，
∴DD′=DB，
∵CD=DB，
∴△BCD′为直角三角形，
∴CD′=2．
故答案为2．
点评：考查最短路线问题；最短路线问题通常是作出一个定点关于相关直线的对称点，连接对称点及另一点的线段即为所求的最短路线长．