题目内容
【题目】正比例函数y1=k1x（k1＞0）与反比例函数y2= 
（k2＞0）部分图象如图所示，则不等式k1x＞ 的解集在数轴上表示正确的是（ ） 
A.
B.
C.
D.
【答案】B
【解析】解：两个函数图象的另一个交点坐标为（﹣2，﹣1），
当﹣2＜x＜0或x＞2时，直线y=k1x在y2= 
图象的上方，
故不等式k1x 
的解集为﹣2＜x＜0或x＞2．
故选：B．
【考点精析】根据题目的已知条件，利用不等式的解集在数轴上的表示的相关知识可以得到问题的答案，需要掌握不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈．
练习册系列答案
相关题目
【题目】小东根据学习函数的经验，对函数y= 
图象与性质进行了探究，下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数y= 的自变量x的取值范围是；
（2）如表是y与x的几组对应值．
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值为；
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出函数y= 的大致图象；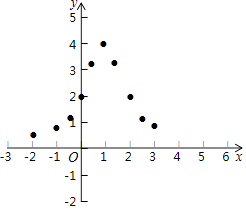 
（4）结合函数图象，请写出函数y= 
的一条性质.
（5）解决问题：如果函数y= 与直线y=a的交点有2个，那么a的取值范围是 ．
