Question

如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长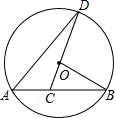CO交⊙O于点D，连接AD．
（1）弦AB=

2

3

（结果保留根号）；
（2）当∠D=20°时，求∠BOD的度数．

Answer 1

分析：（1）如图，过O作OE⊥AB于E，根据垂径定理知道E是AB的中点，然后在Rt△OEB中利用已知条件即可求解；
（2）首先根据三角形的外角和内角的故选得到可以得到∠BOD=∠B+∠A+∠D，接着利用圆周角和圆心角的关系和已知条件即可求出∠BOD的度数．

解答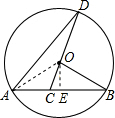：解：（1）如图，过O作OE⊥AB于E，
∴E是AB的中点，
 在Rt△OEB中，OB=2，∠B=30°，
∴OE=1，
∴BE=

3

，
∴AB=2BE=2

3

；

（2）解法一：∵∠BOD=∠B+∠BCO，∠BCO=∠A+∠D．
∴∠BOD=∠B+∠A+∠D． …（3分）
又∵∠BOD=2∠A，∠B=30°，∠D=20°，
∴2∠A=∠B+∠A+∠D=∠A+50°，∠A=50°，…（4分）
∴∠BOD=2∠A=100°．…（5分）
解法二：如图，连接OA．
∵OA=OB，OA=OD，
∴∠BAO=∠B，∠DAO=∠D，
∴∠DAB=∠BAO+∠DAO=∠B+∠D． …（3分）
又∵∠B=30°，∠D=20°，
∴∠DAB=50°，…（4分）
∴∠BOD=2∠DAB=100°（同弧所对的圆周角等于它所对圆心角的一半）．  …（5分）

点评：此题综合考查了垂径定理、解直角三角形的应用及三角形的外角和内角的关系，同时也利用勾股定理进行计算．