题目内容
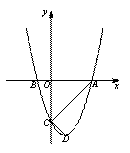
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴交于A、B两点,点A在点B的右侧,且点B的坐标为(-1,0),与y轴的负半轴交于点C,顶点为D.连接AC、CD,∠ACD=90°.
(1)求抛物线的解析式;
(2)点E在抛物线的对称轴上,点F在抛物线上,且以B、A、F、E四点为顶点的四边形为平行四边形,求点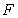 的坐标.
的坐标.
解:(1)∵抛物线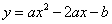 过点B(
过点B(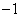 ,0),
,0),
∴a+2a-b=0,∴b=3a,∴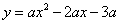
令y=0,则x=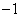 或x=3,∴A(3,0),∴OA=3,
或x=3,∴A(3,0),∴OA=3,
令x=0,则y=-3a,∴C(0,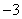 a),∴OC=3a
a),∴OC=3a
 ∵D为抛物线
∵D为抛物线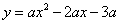 的顶点,∴D(1,
的顶点,∴D(1, 4a)
4a)
过点D作DM⊥y轴于点M,则∠AOC=∠CMD=90°,
又∵∠ACD+∠MCD=∠AOC+∠1,∠ACD=∠AOC=90°
∴∠MCD=∠1 ,∴△AOC∽△CMD,∴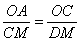 ,
,
∵D(1, 4a),∴DM=1,OM=4a,∴CM=a
4a),∴DM=1,OM=4a,∴CM=a
∴ ,∴
,∴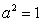 ,∵a>0,∴a=1
,∵a>0,∴a=1
∴抛物线的解析式为: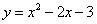
(2)当AB为平行四边形的边时,则BA∥EF,并且EF= BA =4
由于对称轴为直线x=1,∴点E的横坐标为1,∴点F的横坐标为5或者 3
3
将x=5代入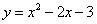 得y=12,∴F(5,12).将x=-3代入
得y=12,∴F(5,12).将x=-3代入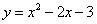 得y=12,∴F(-3,12).
得y=12,∴F(-3,12).
当AB为平行四边形的对角线时,点F即为点D, ∴F(1, 4).
4).
综上所述,点F的坐标为(5,12),( 3,12)或(1,
3,12)或(1, 4).
4).

练习册系列答案
相关题目
 垂线段;
垂线段; 在直线的距离 .
在直线的距离 .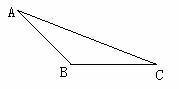
 有意义,则
有意义,则 的取值范围是
的取值范围是 B.
B. C.
C. 与点
与点 重合,点N到达点
重合,点N到达点 时运动终止),过点M、N分别作
时运动终止),过点M、N分别作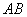 边的垂线,与△ABC的其他边交于P、Q两点,线段MN运动的时间为
边的垂线,与△ABC的其他边交于P、Q两点,线段MN运动的时间为 秒.
秒.
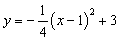 与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.
与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.点P在抛物线上,直线PQ//BC交x轴于点Q,连接BQ.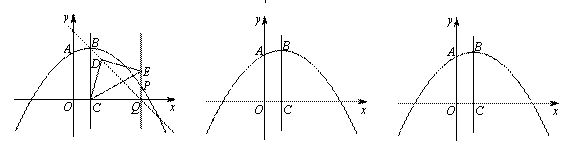
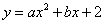 与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.www.12999.com
与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.www.12999.com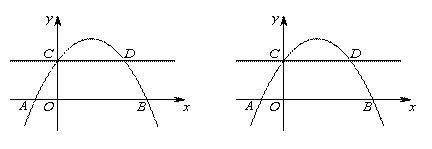 (3)过点P作直线CD的垂线,垂足为Q.若将△CPQ沿CP翻折,点Q的对应点为Q′,是否存在点P,使点Q′恰好在x轴上?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)过点P作直线CD的垂线,垂足为Q.若将△CPQ沿CP翻折,点Q的对应点为Q′,是否存在点P,使点Q′恰好在x轴上?若存在,求出此时点P的坐标;若不存在,请说明理由. 的直径,弦CD⊥AB于点E,点P在
的直径,弦CD⊥AB于点E,点P在 ,求
,求
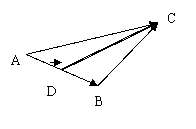
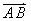 ,已知
,已知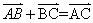 ,如下图所示:如果
,如下图所示:如果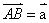 ,
,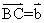 ,则
,则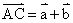 。若D为AB的中点,
。若D为AB的中点,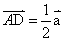 ,若BE为AC上的中线,则用
,若BE为AC上的中线,则用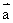 ,
,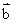 表示
表示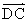 为__________________。
为__________________。